Representation theory of the symmetric group
Encyclopedia
In mathematics
, the representation theory of the symmetric group is a particular case of the representation theory of finite groups
, for which a concrete and detailed theory can be obtained. This has a large area of potential applications, from symmetric function
theory to problems of quantum mechanics
for a number of identical particles
.
The symmetric group
Sn has order n!. Its conjugacy class
es are labeled by partitions of n. Therefore according to the representation theory of a finite group, the number of inequivalent irreducible representations, over the complex number
s, is equal to the number of partitions of n. Unlike the general situation for finite groups, there is in fact a natural way to parametrize irreducible representations by the same set that parametrizes conjugacy classes, namely by partitions of n or equivalently Young diagrams of size n.
Each such irreducible representation can in fact be realized over the integers (every permutation acting by a matrix with integer coefficients); it can be explicitly constructed by computing the Young symmetrizer
s acting on a space generated by the Young tableau
x of shape given by the Young diagram.
Over other field
s the situation can become much more complicated. If the field K has characteristic
equal to zero or greater than n then by Maschke's theorem
the group algebra
KSn is semisimple. In these cases the irreducible representations defined over the integers give the complete set of irreducible representations (after reduction modulo the characteristic if necessary).
However, the irreducible representations of the symmetric group are not known in arbitrary characteristic. In this context it is more usual to use the language of module
s rather than representations. The representation obtained from an irreducible representation defined over the integers by reducing modulo the characteristic will not in general be irreducible. The modules so constructed are called Specht modules, and every irreducible does arise inside some such module. There are now fewer irreducibles, and although they can be classified they are very poorly understood. For example, even their dimension
s are not known in general.
The determination of the irreducible modules for the symmetric group over an arbitrary field is widely regarded as one of the most important open problems in representation theory.
Every symmetric group has a one-dimensional representation called the trivial representation, where every element acts as the one by one identity matrix. For n ≥ 2, there is another irreducible representation of degree 1, called the sign representation or alternating character, which takes a permutation to the one by one matrix with entry ±1 based on the sign of the permutation. These are the only one-dimensional representations of the symmetric groups, as one-dimensional representations are abelian, and the abelianization of the symmetric group is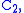
the cyclic group
of order 2.
For all n, there is an n-dimensional representation of the symmetric group of order n, called the , which consists of permuting n coordinates. This has the trivial subrepresentation consisting of vectors whose coordinates are all equal. The orthogonal complement consists of those vectors whose coordinates sum to zero, and when n ≥ 2, the representation on this subspace is an n—1 dimensional irreducible representation. Another n−1 dimensional irreducible representation is found by tensoring with the sign representation.
For n ≥ 7, these are the lowest-dimensional irreducible representations of Sn – all other irreducible representations have dimension at least n. However for n = 4, the surjection from S4 to S3 allows S4 to inherit a two-dimensional irreducible representation. For n = 6, the exceptional transitive embedding of S5 into S6 produces another pair of five-dimensional irreducible representations.
The representation theory of the alternating groups is similar, though the sign representation disappears. For n ≥ 7, the lowest dimensional irreducible representations are the trivial representation in dimension one, and the 
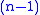-dimensional representation from the other summand of the permutation representation, with all other irreducible representations having higher dimension, but there are exceptions for smaller n.
The alternating groups for n ≥ 5 have only one one-dimensional irreducible representation, the trivial representation. For n = 3, 4 there are two additional one-dimensional irreducible representations, corresponding to maps to the cyclic group of order 3:
and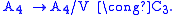 
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the representation theory of the symmetric group is a particular case of the representation theory of finite groups
Representation theory of finite groups
In mathematics, representation theory is a technique for analyzing abstract groups in terms of groups of linear transformations. See the article on group representations for an introduction...
, for which a concrete and detailed theory can be obtained. This has a large area of potential applications, from symmetric function
Symmetric function
In algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
theory to problems of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
for a number of identical particles
Identical particles
Identical particles, or indistinguishable particles, are particles that cannot be distinguished from one another, even in principle. Species of identical particles include elementary particles such as electrons, and, with some clauses, composite particles such as atoms and molecules.There are two...
.
The symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn has order n!. Its conjugacy class
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
es are labeled by partitions of n. Therefore according to the representation theory of a finite group, the number of inequivalent irreducible representations, over the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, is equal to the number of partitions of n. Unlike the general situation for finite groups, there is in fact a natural way to parametrize irreducible representations by the same set that parametrizes conjugacy classes, namely by partitions of n or equivalently Young diagrams of size n.
Each such irreducible representation can in fact be realized over the integers (every permutation acting by a matrix with integer coefficients); it can be explicitly constructed by computing the Young symmetrizer
Young symmetrizer
In mathematics, a Young symmetrizer is an element of the group algebra of the symmetric group, constructed in such a way that the image of the element corresponds to an irreducible representation of the symmetric group over the complex numbers. A similar construction works over any field, and the...
s acting on a space generated by the Young tableau
Young tableau
In mathematics, a Young tableau is a combinatorial object useful in representation theory. It provides a convenient way to describe the group representations of the symmetric and general linear groups and to study their properties. Young tableaux were introduced by Alfred Young, a mathematician at...
x of shape given by the Young diagram.
Over other field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s the situation can become much more complicated. If the field K has characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
equal to zero or greater than n then by Maschke's theorem
Maschke's theorem
In mathematics, Maschke's theorem, named after Heinrich Maschke, is a theorem in group representation theory that concerns the decomposition of representations of a finite group into irreducible pieces...
the group algebra
Group algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
KSn is semisimple. In these cases the irreducible representations defined over the integers give the complete set of irreducible representations (after reduction modulo the characteristic if necessary).
However, the irreducible representations of the symmetric group are not known in arbitrary characteristic. In this context it is more usual to use the language of module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
s rather than representations. The representation obtained from an irreducible representation defined over the integers by reducing modulo the characteristic will not in general be irreducible. The modules so constructed are called Specht modules, and every irreducible does arise inside some such module. There are now fewer irreducibles, and although they can be classified they are very poorly understood. For example, even their dimension
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
s are not known in general.
The determination of the irreducible modules for the symmetric group over an arbitrary field is widely regarded as one of the most important open problems in representation theory.
Low dimensional representations
The lowest dimensional representations of the symmetric groups can be described explicitly, as done in . This work was extended to the smallest k degrees (explicitly for k=4, and k=7) in , and over arbitrary fields in . The smallest two degrees in characteristic zero are described here:Every symmetric group has a one-dimensional representation called the trivial representation, where every element acts as the one by one identity matrix. For n ≥ 2, there is another irreducible representation of degree 1, called the sign representation or alternating character, which takes a permutation to the one by one matrix with entry ±1 based on the sign of the permutation. These are the only one-dimensional representations of the symmetric groups, as one-dimensional representations are abelian, and the abelianization of the symmetric group is
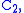the cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order 2.
For all n, there is an n-dimensional representation of the symmetric group of order n, called the , which consists of permuting n coordinates. This has the trivial subrepresentation consisting of vectors whose coordinates are all equal. The orthogonal complement consists of those vectors whose coordinates sum to zero, and when n ≥ 2, the representation on this subspace is an n—1 dimensional irreducible representation. Another n−1 dimensional irreducible representation is found by tensoring with the sign representation.
For n ≥ 7, these are the lowest-dimensional irreducible representations of Sn – all other irreducible representations have dimension at least n. However for n = 4, the surjection from S4 to S3 allows S4 to inherit a two-dimensional irreducible representation. For n = 6, the exceptional transitive embedding of S5 into S6 produces another pair of five-dimensional irreducible representations.
Alternating group
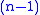-dimensional representation from the other summand of the permutation representation, with all other irreducible representations having higher dimension, but there are exceptions for smaller n.The alternating groups for n ≥ 5 have only one one-dimensional irreducible representation, the trivial representation. For n = 3, 4 there are two additional one-dimensional irreducible representations, corresponding to maps to the cyclic group of order 3:
and 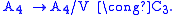- For n ≥ 7, there is just one irreducible representation of degree n − 1, and this is the smallest degree of a non-trivial irreducible representation.
- For n = 3 the obvious analogue of the (n − 1)-dimensional representation is reducible – the permutation representation coincides with the regular representation, and thus breaks up into the three one-dimensional representations, as
is abelian; see the discrete Fourier transformDiscrete Fourier transformIn mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
for representation theory of cyclic groups. - For n = 4, there is just one n − 1 irreducible representation, but there are the exceptional irreducible representations of dimension 1.
- For n = 5, there are two dual irreducible representations of dimension 3, corresponding to its action as icosahedral symmetryIcosahedral symmetryA regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
. - For n = 6, there is an extra irreducible representation of dimension 5 corresponding to the exceptional transitive embedding of A5 in A6.
See also
- Alternating polynomials
- Symmetric polynomials
- Schur functorSchur functorIn mathematics, especially in the field of representation theory, a Schur functor is a functor from the category of modules over a fixed commutative ring to itself. Schur functors are indexed by partitions and are described as follows. Let R be a commutative ring, E an R moduleand λ a partition of...
- Robinson–Schensted correspondence
- Schur–Weyl dualitySchur–Weyl dualitySchur–Weyl duality is a mathematical theorem in representation theory that relates irreducible finite-dimensional representations of the general linear and symmetric groups...
- Jucys–Murphy element