
Riemannian submersion
Encyclopedia
In differential geometry, a branch of mathematics
, a Riemannian submersion is a submersion
from one Riemannian manifold
to another that respects the metrics, meaning that it is an orthogonal projection on tangent spaces.
Let (M, g) and (N, h) be two Riemannian manifolds and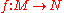
a submersion.
Then f is a Riemannian submersion if and only if the isomorphism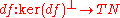
is an isometry
.
 acts isometrically, freely and properly on a Riemannian manifold
acts isometrically, freely and properly on a Riemannian manifold 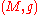 .
.
The projection to the quotient space
to the quotient space
 equipped with the quotient metric is a Riemannian submersion.
equipped with the quotient metric is a Riemannian submersion.
For example, component-wise multiplication on by the group of unit complex numbers yields the Hopf fibration.
by the group of unit complex numbers yields the Hopf fibration.
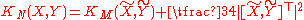
where are orthonormal vector fields on
are orthonormal vector fields on  ,
, 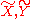 their horizontal lifts to
their horizontal lifts to  ,
,  is the Lie brackets and
is the Lie brackets and  is the projection of the vector field
is the projection of the vector field  to the vertical distribution.
to the vertical distribution.
In particular the lower bound for the sectional curvature of is at least as big as the lower bound for the sectional curvature of
is at least as big as the lower bound for the sectional curvature of  .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Riemannian submersion is a submersion
Submersion (mathematics)
In mathematics, a submersion is a differentiable map between differentiable manifolds whose differential is everywhere surjective. This is a basic concept in differential topology...
from one Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
to another that respects the metrics, meaning that it is an orthogonal projection on tangent spaces.
Let (M, g) and (N, h) be two Riemannian manifolds and
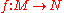
a submersion.
Then f is a Riemannian submersion if and only if the isomorphism
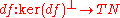
is an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
.
Examples
An example of a Riemannian submersion arises when a Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
 acts isometrically, freely and properly on a Riemannian manifold
acts isometrically, freely and properly on a Riemannian manifold 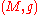 .
.The projection
 to the quotient space
to the quotient spaceQuotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
 equipped with the quotient metric is a Riemannian submersion.
equipped with the quotient metric is a Riemannian submersion.For example, component-wise multiplication on
 by the group of unit complex numbers yields the Hopf fibration.
by the group of unit complex numbers yields the Hopf fibration.Properties
The sectional curvature of the target space of a Riemannian submersion can be calculated from the curvature of the total space by O'Neill's formula: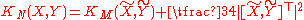
where
 are orthonormal vector fields on
are orthonormal vector fields on  ,
, 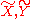 their horizontal lifts to
their horizontal lifts to  ,
,  is the Lie brackets and
is the Lie brackets and  is the projection of the vector field
is the projection of the vector field  to the vertical distribution.
to the vertical distribution.In particular the lower bound for the sectional curvature of
 is at least as big as the lower bound for the sectional curvature of
is at least as big as the lower bound for the sectional curvature of  .
.

