
Robust measures of scale
Encyclopedia
In statistics
, a robust measure of scale is a robust statistic
that quantifies the statistical dispersion
in a set of quantitative
data
. Robust measures of scale
are used to complement or replace conventional estimates of scale such as the sample variance
or sample standard deviation
. As with other robust statistics, a robust measure of scale is minimally affected by a small fraction of outlier
s, at the cost of lower statistical efficiency
when outliers are not present.
(IQR) and the median absolute deviation
(MAD). The IQR is the difference between the 75th percentile
and the 25th percentile
of a sample. The interdecile range
is a robust measure of scale that is closely related to the IQR. The MAD is the median
of the absolute values of the differences between the data values and the overall median of the data set.
They propose two alternative statistics based on pairwise differences: Sn and Qn, defined as:
These can be computed in O(n log n) time and O(n) space.
Neither of these requires location
estimation, as they are based only on differences between values. They are both more efficient than the MAD under a Gaussian distribution: Sn is 58% efficient, while Qn is 82% efficient.
For a large normal sample, 2.219Qn is approximately unbiased for the population standard deviation. For small or moderate samples, the expected value of Qn under a normal distribution depends markedly on the sample size, so finite sample correction factors obtained from a table or from simulations are used to calibrate the scale of Qn.
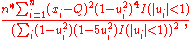
where I is the indicator function, Q is the sample median of the Xi, and

Its square root is a robust estimator of scale, since data points are downweighted as their distance from the median increases, with points more than 9 MAD units from the median having no influence at all.
. For example, the IQR is sometimes defined as the difference between the 75th and 25th percentiles divided by 1.349, so that it becomes unbiased for the population variance if the data follow a normal distribution.
In other situations, it makes more sense to think of a robust measure of scale as an estimator of its own expected value
, interpreted as an alternative to the population variance or standard deviation as a measure of scale. For example, the MAD of a sample from a standard Cauchy distribution
is an estimator of the population MAD, which in this case is 1, whereas the population variance does not exist.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a robust measure of scale is a robust statistic
Robust statistics
Robust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
that quantifies the statistical dispersion
Statistical dispersion
In statistics, statistical dispersion is variability or spread in a variable or a probability distribution...
in a set of quantitative
Quantitative research
In the social sciences, quantitative research refers to the systematic empirical investigation of social phenomena via statistical, mathematical or computational techniques. The objective of quantitative research is to develop and employ mathematical models, theories and/or hypotheses pertaining to...
data
Data
The term data refers to qualitative or quantitative attributes of a variable or set of variables. Data are typically the results of measurements and can be the basis of graphs, images, or observations of a set of variables. Data are often viewed as the lowest level of abstraction from which...
. Robust measures of scale
Scale parameter
In probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions...
are used to complement or replace conventional estimates of scale such as the sample variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
or sample standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
. As with other robust statistics, a robust measure of scale is minimally affected by a small fraction of outlier
Outlier
In statistics, an outlier is an observation that is numerically distant from the rest of the data. Grubbs defined an outlier as: An outlying observation, or outlier, is one that appears to deviate markedly from other members of the sample in which it occurs....
s, at the cost of lower statistical efficiency
Efficiency (statistics)
In statistics, an efficient estimator is an estimator that estimates the quantity of interest in some “best possible” manner. The notion of “best possible” relies upon the choice of a particular loss function — the function which quantifies the relative degree of undesirability of estimation errors...
when outliers are not present.
IQR and MAD
The most familiar robust measures of scale are the interquartile rangeInterquartile range
In descriptive statistics, the interquartile range , also called the midspread or middle fifty, is a measure of statistical dispersion, being equal to the difference between the upper and lower quartiles...
(IQR) and the median absolute deviation
Median absolute deviation
In statistics, the median absolute deviation is a robust measure of the variability of a univariate sample of quantitative data. It can also refer to the population parameter that is estimated by the MAD calculated from a sample....
(MAD). The IQR is the difference between the 75th percentile
Percentile
In statistics, a percentile is the value of a variable below which a certain percent of observations fall. For example, the 20th percentile is the value below which 20 percent of the observations may be found...
and the 25th percentile
Percentile
In statistics, a percentile is the value of a variable below which a certain percent of observations fall. For example, the 20th percentile is the value below which 20 percent of the observations may be found...
of a sample. The interdecile range
Interdecile range
In statistics, the interdecile range is the difference between the first and the ninth deciles . The interdecile range is a measure of statistical dispersion of the values in a set of data, similar to the range and the interquartile range....
is a robust measure of scale that is closely related to the IQR. The MAD is the median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
of the absolute values of the differences between the data values and the overall median of the data set.
Robust measures of scale based on absolute pairwise differences
Rousseeuw and Croux propose alternatives to the MAD, motivated by two weaknesses of it:- It is inefficientEfficiency (statistics)In statistics, an efficient estimator is an estimator that estimates the quantity of interest in some “best possible” manner. The notion of “best possible” relies upon the choice of a particular loss function — the function which quantifies the relative degree of undesirability of estimation errors...
(37% efficiency) at Gaussian distributions. - it computes a symmetric statistic about a location estimate, thus not dealing with skewnessSkewnessIn probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
.
They propose two alternative statistics based on pairwise differences: Sn and Qn, defined as:

These can be computed in O(n log n) time and O(n) space.
Neither of these requires location
Location parameter
In statistics, a location family is a class of probability distributions that is parametrized by a scalar- or vector-valued parameter μ, which determines the "location" or shift of the distribution...
estimation, as they are based only on differences between values. They are both more efficient than the MAD under a Gaussian distribution: Sn is 58% efficient, while Qn is 82% efficient.
For a large normal sample, 2.219Qn is approximately unbiased for the population standard deviation. For small or moderate samples, the expected value of Qn under a normal distribution depends markedly on the sample size, so finite sample correction factors obtained from a table or from simulations are used to calibrate the scale of Qn.
The biweight midvariance
Like Sn and Qn, the biweight midvariance aims to be robust without sacrificing too much efficiency. It is defined as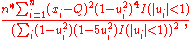
where I is the indicator function, Q is the sample median of the Xi, and

Its square root is a robust estimator of scale, since data points are downweighted as their distance from the median increases, with points more than 9 MAD units from the median having no influence at all.
The population analogue of a robust measure of scale
In some cases, robust estimators of scale are used to estimate the population variance or population standard deviationStandard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
. For example, the IQR is sometimes defined as the difference between the 75th and 25th percentiles divided by 1.349, so that it becomes unbiased for the population variance if the data follow a normal distribution.
In other situations, it makes more sense to think of a robust measure of scale as an estimator of its own expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
, interpreted as an alternative to the population variance or standard deviation as a measure of scale. For example, the MAD of a sample from a standard Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
is an estimator of the population MAD, which in this case is 1, whereas the population variance does not exist.

