Ryll-Nardzewski fixed point theorem
Encyclopedia
In functional analysis
, a branch of mathematics, the Ryll-Nardzewski fixed-point theorem states that if
is a normed vector space
and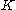
is a nonempty convex
subset of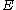
which is compact
under the weak topology
, then every group
(or equivalently: every semigroup
) of affine isometries
of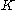
has at least one fixed point. (Here, a fixed point of a set of maps is a point that is fixed
by each map in the set.)
This theorem was announced by Czesław Ryll-Nardzewski. Later Namioka and Asplund gave a proof based on a different approach. Ryll-Nardzewski himself gave a complete proof in the original spirit.
on compact groups.
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, a branch of mathematics, the Ryll-Nardzewski fixed-point theorem states that if
is a normed vector spaceNormed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
and
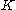is a nonempty convexConvex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
subset of
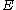which is compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
under the weak topology
Weak topology
In mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
, then every group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
(or equivalently: every semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
) of affine isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of
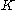has at least one fixed point. (Here, a fixed point of a set of maps is a point that is fixedFixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
by each map in the set.)
This theorem was announced by Czesław Ryll-Nardzewski. Later Namioka and Asplund gave a proof based on a different approach. Ryll-Nardzewski himself gave a complete proof in the original spirit.
Applications
The Ryll-Nardzewski theorem yields the existence of a Haar measureHaar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
on compact groups.