In modal logic

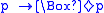
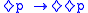
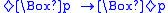
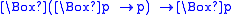
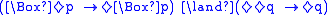
Modal logic

Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...

, Sahlqvist formulas are a certain kind of modal formula with remarkable properties. The Sahlqvist correspondence theorem states that every Sahlqvist formula is canonical, and corresponds to a first-order

First-order logic

First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...

 definable class of Kripke frames

Kripke semantics

Kripke semantics is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke. It was first made for modal logics, and later adapted to intuitionistic logic and other non-classical systems...

.

Sahlqvist's definition characterizes a decidable set of modal formulas with first-order correspondents. Since it is undecidable, by Chagrova's theorem, whether an arbitrary modal formula has a first-order correspondent, there are formulas with first-order frame conditions that are not Sahlqvist [Chagrova 1991] (see the examples below). Hence Sahlqvist formulas define only a (decidable) subset of modal formulas with first-order correspondents.

Definition

Sahlqvist formulas are built up from implications, where the consequent is positive and the antecedent is of a restricted form.

• A boxed atom is a propositional atom preceded by a number (possibly 0) of boxes, i.e. a formula of the form (often abbreviated as 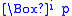for ).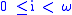
• A Sahlqvist antecedent is a formula constructed using ∧, ∨, and from boxed atoms, and negative formulas (including the constants ⊥, ⊤).
• A Sahlqvist implication is a formula A → B, where A is a Sahlqvist antecedent, and B is a positive formula.
• A Sahlqvist formula is constructed from Sahlqvist antecedents using ∧ and (unlimited), and using ∨ on formulas with no common variables.

Examples of Sahlqvist formulas

Its first-order corresponding formula is , and it defines all reflexive frames

Reflexive relation

In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...

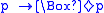
Its first-order corresponding formula is , and it defines all symmetric frames

Symmetric relation

In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...

Its first-order corresponding formula is 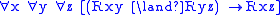, and it defines all transitive frames

Transitive relation

In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....

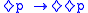
Its first-order corresponding formula is 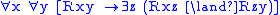, and it defines all dense frames

Dense order

In mathematics, a partial order ≤ on a set X is said to be dense if, for all x and y in X for which x In mathematics, a partial order ≤ on a set X is said to be dense if, for all x and y in X for which x...

Its first-order corresponding formula is , and it defines all right-unbounded frames

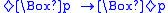
Its first-order corresponding formula is 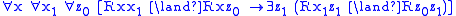, and it is the Church-Rosser property

Church–Rosser theorem

The Church–Rosser theorem states that if there are two distinct reductions starting from the same lambda calculus term, then there exists a term that is reachable from each reduct via a sequence of reductions...

.

Examples of non-Sahlqvist formulas

This is the McKinsey formula and it does not have a first-order frame condition, hence it is not Sahlqvist

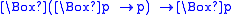
The Löb axiom is not Sahlqvist, again because it does not have a first-order frame condition

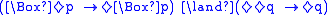
The conjunction of the McKinsey formula and the (4) axiom has a first-order frame condition but is not equivalent to any Sahlqvist formula.

Kracht's theorem

When a Sahlqvist formula is used as an axiom in a normal modal logic, the logic is guaranteed to be complete with respect to the elementary class of frames the axiom defines. This result comes from the Sahlqvist completeness theorem [Modal Logic, Blackburn et. al., Theorem 4.42]. But there is also a converse theorem, namely a theorem that states which first-order conditions are the correspondents of Sahlqvist formulas. Kracht's theorem states that any Sahlqvist formula locally corresponds to a Kracht formula; and conversely, every Kracht formula is a local first-order correspondent of some Sahlqvist formula which can be effectively obtained from the Kracht formula [Modal Logic, Blackburn et. al., Theorem 3.59].