Scalar theories of gravitation
Encyclopedia
Scalar theories of gravitation are field theories of gravitation
in which the gravitational field is described using a scalar field
, which is required to satisfy some field equation.
Note: This article focuses on relativistic
classical field theories
of gravitation. The best known relativistic classical field theory of gravitation, general relativity
, is a tensor theory, in which the gravitational interaction is described using a tensor
field.
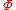, which is required to satisfy the Poisson equation (with the mass density acting as the source of the field). To wit:
, where
This field theory formulation leads directly to the familiar law of universal gravitation,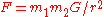
.
created two such theories.
Nordström's first idea (1912) was to simply replace the divergence operator in the field equation of Newtonian gravity with the d'Alembertian
operator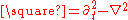
. This gives the field equation
.
However, several theoretical difficulties with this theory quickly arose, and Nordström dropped it.
A year later, Nordström tried again, presenting the field equation
,
where
is the trace of the stress-energy tensor
.
Solutions of Nordström's second theory are conformally flat
Lorentzian spacetimes. That is, the metric tensor can be written as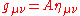
, where
This suggestion signifies that the inertial mass should depend on the scalar field.
Nordström's second theory satisfies the weak equivalence principle
. However:
Despite these disappointing results, Einstein's critiques of Nordström's second theory played an important role in his development of general relativity.
that general covariance was not viable. Inspired by Nordström's work, he proposed his own scalar theory. This theory employs a massless scalar field coupled to the stress-energy tensor, which is the sum of two terms. The first,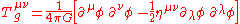
represents the stress-momentum-energy of the scalar field itself. The second represents the stress-momentum-energy of any matter which may be present: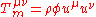
where
is the velocity
vector of an observer, or tangent vector
to the world line of the observer. (Einstein made no attempt, in this theory, to take account of possible gravitational effects of the field energy of the electromagnetic field
.)
Unfortunately, this theory is not diffeomorphism
covariant. This is an important consistency condition, so Einstein dropped this theory in late 1914. Associating the scalar field with the metric leads to Einstein's later conclusions that the theory of gravitation he sought could not be a scalar theory. Indeed, the theory he finally arrived at in 1915, general relativity
, is a tensor theory, not a scalar theory, with a 2-tensor, the metric, as the potential. Unlike his 1913 scalar theory, it is generally covariant, and it does take into account the field energy-momentum-stress of the electromagnetic field (or any other nongravitational field).
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
in which the gravitational field is described using a scalar field
Scalar field theory
In theoretical physics, scalar field theory can refer to a classical or quantum theory of scalar fields. A field which is invariant under any Lorentz transformation is called a "scalar", in contrast to a vector or tensor field...
, which is required to satisfy some field equation.
Note: This article focuses on relativistic
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
classical field theories
Classical field theory
A classical field theory is a physical theory that describes the study of how one or more physical fields interact with matter. The word 'classical' is used in contrast to those field theories that incorporate quantum mechanics ....
of gravitation. The best known relativistic classical field theory of gravitation, general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, is a tensor theory, in which the gravitational interaction is described using a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
field.
Newtonian gravity
The prototypical scalar theory of gravitation is Newtonian gravitation. In this theory, the gravitational interaction is completely described by the potentialPotential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
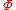, which is required to satisfy the Poisson equation (with the mass density acting as the source of the field). To wit:, where
- G is the gravitational constant and
-
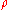is the mass density.
This field theory formulation leads directly to the familiar law of universal gravitation,
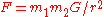.Nordström's theories of gravitation
The first attempts to present a relativistic (classical) field theory of gravitation were also scalar theories. Gunnar NordströmGunnar Nordström
Gunnar Nordström was a Finnish theoretical physicist best remembered for his theory of gravitation, which was an early competitor of general relativity...
created two such theories.
Nordström's first idea (1912) was to simply replace the divergence operator in the field equation of Newtonian gravity with the d'Alembertian
D'Alembert operator
In special relativity, electromagnetism and wave theory, the d'Alembert operator , also called the d'Alembertian or the wave operator, is the Laplace operator of Minkowski space. The operator is named for French mathematician and physicist Jean le Rond d'Alembert...
operator
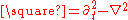. This gives the field equation.However, several theoretical difficulties with this theory quickly arose, and Nordström dropped it.
A year later, Nordström tried again, presenting the field equation
,where
is the trace of the stress-energy tensorStress-energy tensor
The stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
.
Solutions of Nordström's second theory are conformally flat
Conformally flat
A Riemannian manifold is conformally flat if each point has a neighborhood that can be mapped to flat space by a conformal transformation.More formally, let be a pseudo-Riemannian manifold...
Lorentzian spacetimes. That is, the metric tensor can be written as
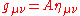, where
- ημν is the Minkowski metric, and
-
is a scalar which is a function of position.
This suggestion signifies that the inertial mass should depend on the scalar field.
Nordström's second theory satisfies the weak equivalence principle
Equivalence principle
In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
. However:
- The theory fails to predict any deflection of light passing near a massive body (contrary to observation)
- The theory predicts an anomalous perihelion precessionPrecessionPrecession is a change in the orientation of the rotation axis of a rotating body. It can be defined as a change in direction of the rotation axis in which the second Euler angle is constant...
of MercuryMercury (planet)Mercury is the innermost and smallest planet in the Solar System, orbiting the Sun once every 87.969 Earth days. The orbit of Mercury has the highest eccentricity of all the Solar System planets, and it has the smallest axial tilt. It completes three rotations about its axis for every two orbits...
, but this disagrees in both sign and magnitude with the observed anomalous precession (the part which cannot be explained using Newtonian gravitation).
Despite these disappointing results, Einstein's critiques of Nordström's second theory played an important role in his development of general relativity.
Einstein's scalar theory
In 1913, Einstein (erroneously) concluded from his hole argumentHole argument
In general relativity, the hole argument is a "paradox" which much troubled Albert Einstein while developing his famous field equation.It is incorrectly interpreted by some philosophers as an argument against manifold substantialism, a doctrine that the manifold of events in spacetime are a...
that general covariance was not viable. Inspired by Nordström's work, he proposed his own scalar theory. This theory employs a massless scalar field coupled to the stress-energy tensor, which is the sum of two terms. The first,
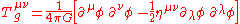
represents the stress-momentum-energy of the scalar field itself. The second represents the stress-momentum-energy of any matter which may be present:
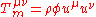
where
is the velocityFour-velocity
In physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
vector of an observer, or tangent vector
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
to the world line of the observer. (Einstein made no attempt, in this theory, to take account of possible gravitational effects of the field energy of the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
.)
Unfortunately, this theory is not diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
covariant. This is an important consistency condition, so Einstein dropped this theory in late 1914. Associating the scalar field with the metric leads to Einstein's later conclusions that the theory of gravitation he sought could not be a scalar theory. Indeed, the theory he finally arrived at in 1915, general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, is a tensor theory, not a scalar theory, with a 2-tensor, the metric, as the potential. Unlike his 1913 scalar theory, it is generally covariant, and it does take into account the field energy-momentum-stress of the electromagnetic field (or any other nongravitational field).
Additional variations
- Kaluza–Klein theoryKaluza–Klein theoryIn physics, Kaluza–Klein theory is a model that seeks to unify the two fundamental forces of gravitation and electromagnetism. The theory was first published in 1921. It was proposed by the mathematician Theodor Kaluza who extended general relativity to a five-dimensional spacetime...
involves the use of a scalar gravitational field in addition to the electromagnetic fieldElectromagnetic fieldAn electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
potential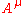
in an attempt to create a five-dimensional unification of gravity and electromagnetism. Its generalization with a 5th variable component of the metric that leads to a variable gravitational constant was first given by Pascual JordanPascual Jordan-Further reading:...
http://www.citebase.org/cgi-bin/fulltext?format=application/pdf&identifier=oai:arXiv.org:gr-qc/0506063. - Brans–Dicke theory is a scalar-tensor theory, not a scalar theory, meaning that it represents the gravitational interaction using both a scalar field and a tensor field. We mention it here because one of the field equations of this theory involves only the scalar field and the trace of the stress-energy tensor, as in Nordström's theory. Moreover, the Brans-Dicke theory is equal to the independently derived theory of Jordan (hence it is often referred to as the Jordan-Brans-Dicke or JBD theory). The Brans-Dicke theory couples a scalar field with the curvature of space-time and is self-consistent and, assuming appropriate values for a tunable constant, this theory has not been ruled out by observation. The Brans-Dicke theory is generally regarded as a leading competitor of general relativity, which is a pure tensor theory. However, the Brans-Dicke theory seems to need too high a parameter, which favours general relativity).
- Zee combined the idea of the BD theory with the Higgs-Mechanism of Symmetry Breakdown for mass generation, which led to a scalar-tensor theory with Higgs field as scalar field, in which the scalar field is massive (short-ranged). An example of this theory was proposed by H. Dehnen and H. Frommert 1991, parting from the nature of Higgs field interacting gravitational- and Yukawa (long-ranged)-like with the particles that get mass through it (Int. J. of Theor. Phys. 29(4): 361, 1990).
- The Watt-Misner theory (1999) is a recent example of a scalar theory of gravitation. It is not intended as a viable theory of gravitation (since, as Watt and Misner point out, it is not consistent with observation), but as a toy theory which can be useful in testing numerical relativity schemes. It also has pedagogical value.