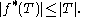Schwarz–Ahlfors–Pick theorem
Encyclopedia
In mathematics
, the Schwarz–Ahlfors–Pick theorem is an extension of the Schwarz lemma
for hyperbolic geometry
, such as the Poincaré half-plane model
. It states that the Poincaré metric
is distance-decreasing on harmonic
functions.
The theorem states that every holomorphic function on the unit disk U, or the upper half-plane H, with distances defined by the Poincaré metric, is a contraction mapping
. That is, every such analytic mapping will not increase the distance between points. Stated more precisely:
Theorem: (Schwarz
–Ahlfors–Pick
) For all holomorphic functions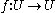
, one has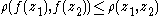 
for points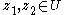
and Poincaré distance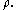 
For any tangent vector
T, the hyperbolic length of the tangent vector does not increase: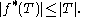
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Schwarz–Ahlfors–Pick theorem is an extension of the Schwarz lemma
Schwarz lemma
In mathematics, the Schwarz lemma, named after Hermann Amandus Schwarz, is a result in complex analysis about holomorphic functions from the open unit disk to itself. The lemma is less celebrated than stronger theorems, such as the Riemann mapping theorem, which it helps to prove...
for hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, such as the Poincaré half-plane model
Poincaré half-plane model
In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane , together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry....
. It states that the Poincaré metric
Poincaré metric
In mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry or Riemann surfaces.There are three equivalent...
is distance-decreasing on harmonic
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
functions.
The theorem states that every holomorphic function on the unit disk U, or the upper half-plane H, with distances defined by the Poincaré metric, is a contraction mapping
Contraction mapping
In mathematics, a contraction mapping, or contraction, on a metric space is a function f from M to itself, with the property that there is some nonnegative real number k...
. That is, every such analytic mapping will not increase the distance between points. Stated more precisely:
Theorem: (Schwarz
Hermann Schwarz
Karl Hermann Amandus Schwarz was a German mathematician, known for his work in complex analysis. He was born in Hermsdorf, Silesia and died in Berlin...
–Ahlfors–Pick
Georg Alexander Pick
Georg Alexander Pick was an Austrian mathematician. He was born to Josefa Schleisinger and Adolf Josef Pick. He died in the Theresienstadt concentration camp. Today he is best known for Pick's formula for determining the area of lattice polygons...
) For all holomorphic functions
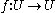, one has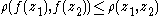 for points
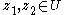and Poincaré distance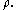 For any tangent vector
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
T, the hyperbolic length of the tangent vector does not increase: