Semi-implicit Euler method
Encyclopedia
In mathematics, the semi-implicit Euler method, also called symplectic Euler, semi-explicit Euler, Euler–Cromer, and Newton–Størmer–Verlet (NSV), is a modification of the Euler method
for solving Hamilton's equations, a system of ordinary differential equation
s that arises in classical mechanics
. It is a symplectic integrator
and hence it yields better results than the standard Euler method.
s of the form
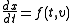
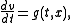
where f and g are given functions. Here, x and v may be either scalars or vectors. The equations of motion in Hamiltonian mechanics
take this form if the Hamiltonian is of the form
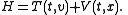
The differential equations are to be solved with the initial condition
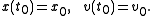
solution by iterating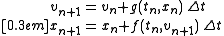
where Δt is the time step and tn = t0 + nΔt is the time after n steps.
The difference with the standard Euler method is that the semi-implicit Euler method uses vn+1 in the equation for xn+1, while the Euler method uses vn.
Applying the method with negative time step to the computation of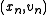
from 
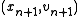and rearranging leads to the second variant of the semi-implicit Euler method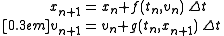
which has similar properties.
The semi-implicit Euler is a first-order integrator, just as the standard Euler method. This means that it commits a global error of the order of Δt. However, the semi-implicit Euler method is a symplectic integrator
, unlike the standard method. As a consequence, the semi-implicit Euler method almost conserves the energy (when the Hamiltonian is time-independent). Often, the energy increases steadily
when the standard Euler method is applied, making it far less accurate.
Alternating between the two variants of the semi-implicit Euler method leads in one simplification to the Störmer-Verlet integration
and in a slightly different simplification to the leapfrog integration
, increasing both the order of the error and the order of preservation of energy.
satisfying Hooke's law
is given by
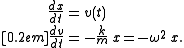
The semi-implicit Euler for this equation is
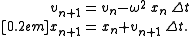
The iteration preserves the modified energy functional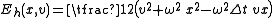
exactly, leading to stable periodic orbits that deviate by 
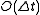from the exact orbits. The exact circular frequency 
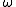increases in the numerical approximation by a factor of 
.
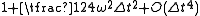Euler integration
In mathematics and computational science, the Euler method, named after Leonhard Euler, is a first-order numerical procedure for solving ordinary differential equations with a given initial value...
for solving Hamilton's equations, a system of ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s that arises in classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
. It is a symplectic integrator
Symplectic integrator
In mathematics, a symplectic integrator is a numerical integration scheme for a specific group of differential equations related to classical mechanics and symplectic geometry. Symplectic integrators form the subclass of geometric integrators which, by definition, are canonical transformations...
and hence it yields better results than the standard Euler method.
Setting
The semi-implicit Euler method can be applied to a pair of differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s of the form
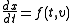
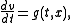
where f and g are given functions. Here, x and v may be either scalars or vectors. The equations of motion in Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
take this form if the Hamiltonian is of the form
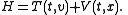
The differential equations are to be solved with the initial condition
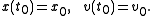
The method
The semi-implicit Euler method produces an approximate discreteDiscrete mathematics
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...
solution by iterating
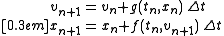
where Δt is the time step and tn = t0 + nΔt is the time after n steps.
The difference with the standard Euler method is that the semi-implicit Euler method uses vn+1 in the equation for xn+1, while the Euler method uses vn.
Applying the method with negative time step to the computation of
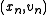from 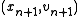and rearranging leads to the second variant of the semi-implicit Euler method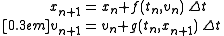which has similar properties.
The semi-implicit Euler is a first-order integrator, just as the standard Euler method. This means that it commits a global error of the order of Δt. However, the semi-implicit Euler method is a symplectic integrator
Symplectic integrator
In mathematics, a symplectic integrator is a numerical integration scheme for a specific group of differential equations related to classical mechanics and symplectic geometry. Symplectic integrators form the subclass of geometric integrators which, by definition, are canonical transformations...
, unlike the standard method. As a consequence, the semi-implicit Euler method almost conserves the energy (when the Hamiltonian is time-independent). Often, the energy increases steadily
Energy drift
In molecular dynamics, orbit, and particle simulations, energy drift is the gradual change in the total energy of a closed system. According to the laws of mechanics, the energy should be a constant of motion and should not change...
when the standard Euler method is applied, making it far less accurate.
Alternating between the two variants of the semi-implicit Euler method leads in one simplification to the Störmer-Verlet integration
Verlet integration
Verlet integration is a numerical method used to integrate Newton's equations of motion. It is frequently used to calculate trajectories of particles in molecular dynamics simulations and computer graphics...
and in a slightly different simplification to the leapfrog integration
Leapfrog integration
Leapfrog integration is a simple method for numerically integrating differential equations of the form\ddot x=F,or equivalently of the form\dot v=F,\;\dot x \equiv v,particularly in the case of a dynamical system of classical mechanics...
, increasing both the order of the error and the order of preservation of energy.
Example
The motion of a springSpring (device)
A spring is an elastic object used to store mechanical energy. Springs are usually made out of spring steel. Small springs can be wound from pre-hardened stock, while larger ones are made from annealed steel and hardened after fabrication...
satisfying Hooke's law
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
is given by
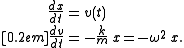
The semi-implicit Euler for this equation is
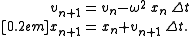
The iteration preserves the modified energy functional
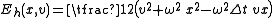exactly, leading to stable periodic orbits that deviate by 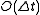from the exact orbits. The exact circular frequency 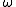increases in the numerical approximation by a factor of .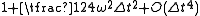