Sequent
Encyclopedia
In proof theory
, a sequent is a formalized
statement of provability
that is frequently used when specifying calculi
for deduction
. In the sequent calculus
, the name sequent is used for the construct which can be regarded as a specific kind of judgment
, characteristic to this deduction system.
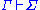
where both Γ and Σ are sequence
s of logical
formulae (i.e., both the number and the order of the occurring formulae matter). The symbol
is usually referred to as turnstile
or tee and is often read, suggestively, as "yields" or "proves". It is not a symbol in the language, rather it is a symbol in the metalanguage
used to discuss proofs. In a sequent, Γ is called the antecedent and Σ is said to be the succedent of the sequent.
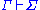is that under the assumption of Γ the conclusion of Σ is provable. Classically, the formulae on the left of the turnstile can be interpreted conjunctively
while the formulae on the right can be considered as a disjunction
. This means that, when all formulae in Γ hold, then at least one formula in Σ also has to be true. If the succedent is empty, this is interpreted as falsity, i.e.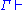
means that Γ proves falsity and is thus inconsistent. On the other hand an empty antecedent is assumed to be true, i.e., 
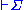means that Σ follows without any assumptions, i.e., it is always true (as a disjunction). A sequent of this form, with Γ empty, is known as a logical assertion
.
Of course, other intuitive explanations are possible, which are classically equivalent. For example,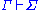
can be read as asserting that it cannot be the case that every formula in Γ is true and every formula in Σ is false (this is related to the double-negation interpretations of classical into intuitionistic logic
, such as Glivenko's theorem
).
In any case, these intuitive readings are only pedagogical. Since formal proofs in proof theory are purely syntactic
, the meaning
of (the derivation of) a sequent is only given by the properties of the calculus that provides the actual rules of inference
.
Barring any contradictions in the technically precise definition above we can describe sequents in their introductory logical form.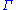
represents a set of assumptions that we begin our logical process with, for example "Socrates is a man" and "All men are mortal". The 
represents a logical conclusion that follows under these premises. For example "Socrates is mortal" follows from a reasonable formalization of the above points and we could expect to see it on the 
side of the turnstile. In this sense, 
means the process of reasoning, or "therefore" in English.
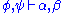
This claims that either
or 
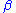can be derived from 
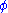and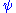 
.
A typical rule is:
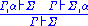
This indicates that if we can deduce that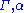
yields 
, and that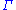 
yields 
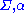, then we can also deduce that 
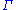yields 
.
. Similarly, one can obtain calculi for dual-intuitionistic logic (a type of paraconsistent logic
) by requiring that sequents be singular in the antecedent.
In many cases, sequents are also assumed to consist of multiset
s or sets instead of sequences. Thus one disregards the order or even the number of occurrences of the formulae. For classical propositional logic this does not yield a problem, since the conclusions that one can draw from a collection of premises does not depend on these data. In substructural logic
, however, this may become quite important.
in order to specify his famous sequent calculus
. In his German publication he used the word "Sequenz". However, in English, the word "sequence
" is already used as a translation to the German "Folge" and appears quite frequently in mathematics. The term "sequent" then has been created in search for an alternative translation of the German expression.
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
, a sequent is a formalized
Formalism (mathematics)
In foundations of mathematics, philosophy of mathematics, and philosophy of logic, formalism is a theory that holds that statements of mathematics and logic can be thought of as statements about the consequences of certain string manipulation rules....
statement of provability
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
that is frequently used when specifying calculi
Proof calculus
In mathematical logic, a proof calculus corresponds to a family of formal systems that use a common style of formal inference for its inference rules...
for deduction
Deductive reasoning
Deductive reasoning, also called deductive logic, is reasoning which constructs or evaluates deductive arguments. Deductive arguments are attempts to show that a conclusion necessarily follows from a set of premises or hypothesis...
. In the sequent calculus
Sequent calculus
In proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
, the name sequent is used for the construct which can be regarded as a specific kind of judgment
Judgment (mathematical logic)
In mathematical logic, a judgment can be for example an assertion about occurrence of a free variable in an expression of the object language, or about provability of a proposition ; but judgments can be also other inductively definable assertions in the metatheory...
, characteristic to this deduction system.
Explanation
A sequent has the form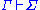where both Γ and Σ are sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s of logical
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
formulae (i.e., both the number and the order of the occurring formulae matter). The symbol
is usually referred to as turnstileTurnstile (symbol)
In mathematical logic and computer science the symbol \vdash has taken the name turnstile because of its resemblance to a typical turnstile if viewed from above. It is also referred to as tee and is often read as "yields", "proves", "satisfies" or "entails"...
or tee and is often read, suggestively, as "yields" or "proves". It is not a symbol in the language, rather it is a symbol in the metalanguage
Metalanguage
Broadly, any metalanguage is language or symbols used when language itself is being discussed or examined. In logic and linguistics, a metalanguage is a language used to make statements about statements in another language...
used to discuss proofs. In a sequent, Γ is called the antecedent and Σ is said to be the succedent of the sequent.
Intuitive meaning
The intuitive meaning of the sequent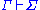 is that under the assumption of Γ the conclusion of Σ is provable. Classically, the formulae on the left of the turnstile can be interpreted conjunctivelyLogical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
while the formulae on the right can be considered as a disjunction
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
. This means that, when all formulae in Γ hold, then at least one formula in Σ also has to be true. If the succedent is empty, this is interpreted as falsity, i.e.
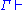means that Γ proves falsity and is thus inconsistent. On the other hand an empty antecedent is assumed to be true, i.e., 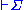means that Σ follows without any assumptions, i.e., it is always true (as a disjunction). A sequent of this form, with Γ empty, is known as a logical assertionLogical assertion
A logical assertion is a statement that asserts that a certain premise is true, and is useful for statements in proof. It is equivalent to a sequent with an empty antecedent....
.
Of course, other intuitive explanations are possible, which are classically equivalent. For example,
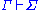can be read as asserting that it cannot be the case that every formula in Γ is true and every formula in Σ is false (this is related to the double-negation interpretations of classical into intuitionistic logicIntuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
, such as Glivenko's theorem
Glivenko's theorem
Glivenko's theorem is a basic result showing a close connection between classical and intuitionistic propositional logic. It was proven by Valery Glivenko in 1929, with the aim of showing that intuitionistic logic is consistent and coherent...
).
In any case, these intuitive readings are only pedagogical. Since formal proofs in proof theory are purely syntactic
Syntax
In linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
, the meaning
Semantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
of (the derivation of) a sequent is only given by the properties of the calculus that provides the actual rules of inference
Rule of inference
In logic, a rule of inference, inference rule, or transformation rule is the act of drawing a conclusion based on the form of premises interpreted as a function which takes premises, analyses their syntax, and returns a conclusion...
.
Barring any contradictions in the technically precise definition above we can describe sequents in their introductory logical form.
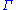represents a set of assumptions that we begin our logical process with, for example "Socrates is a man" and "All men are mortal". The represents a logical conclusion that follows under these premises. For example "Socrates is mortal" follows from a reasonable formalization of the above points and we could expect to see it on the side of the turnstile. In this sense, means the process of reasoning, or "therefore" in English.Example
A typical sequent might be: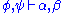This claims that either
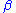or can be derived from 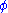and 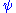.Property
Since every formula in the antecedent (the left side) must be true to conclude the truth of at least one formula in the succedent (the right side), adding formulas to either side results in a weaker sequent, while removing them from either side gives a stronger one.Rules
Most proof systems provide ways to deduce one sequent from another. These inference rules are written with a list of sequents above and below a line. This rule indicates that if everything above the line is true, so is everything under the line.A typical rule is:
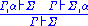
This indicates that if we can deduce that
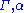yields , and that 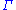yields 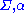, then we can also deduce that 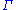yields .Variations
The general notion of sequent introduced here can be specialized in various ways. A sequent is said to be an intuitionistic sequent if there is at most one formula in the succedent. This form is needed to obtain calculi for intuitionistic logicIntuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
. Similarly, one can obtain calculi for dual-intuitionistic logic (a type of paraconsistent logic
Paraconsistent logic
A paraconsistent logic is a logical system that attempts to deal with contradictions in a discriminating way. Alternatively, paraconsistent logic is the subfield of logic that is concerned with studying and developing paraconsistent systems of logic.Inconsistency-tolerant logics have been...
) by requiring that sequents be singular in the antecedent.
In many cases, sequents are also assumed to consist of multiset
Multiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
s or sets instead of sequences. Thus one disregards the order or even the number of occurrences of the formulae. For classical propositional logic this does not yield a problem, since the conclusions that one can draw from a collection of premises does not depend on these data. In substructural logic
Substructural logic
In logic, a substructural logic is a logic lacking one of the usual structural rules , such as weakening, contraction or associativity...
, however, this may become quite important.
History
Historically, sequents have been introduced by Gerhard GentzenGerhard Gentzen
Gerhard Karl Erich Gentzen was a German mathematician and logician. He had his major contributions in the foundations of mathematics, proof theory, especially on natural deduction and sequent calculus...
in order to specify his famous sequent calculus
Sequent calculus
In proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
. In his German publication he used the word "Sequenz". However, in English, the word "sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
" is already used as a translation to the German "Folge" and appears quite frequently in mathematics. The term "sequent" then has been created in search for an alternative translation of the German expression.