Sequential Minimal Optimization
Encyclopedia
Sequential minimal optimization (SMO) is an algorithm for efficiently solving the optimization problem which arises during the training of support vector machine
s. It was invented by John Platt
in 1998 at Microsoft Research
. SMO is widely used for training support vector machines and is implemented by the popular libsvm tool. The publication of the SMO algorithm in 1998 has generated a lot of excitement in the SVM community, as previously available methods for SVM training were much more complex and required expensive third-party QP
solvers.
problem with a dataset (x1, y1), ..., (xn, yn), where xi is an input vector and is a binary label corresponding to it. A soft-margin support vector machine
is trained by solving a quadratic programming problem, which is expressed in the dual form
as follows:
where C is an SVM hyperparameter and K(xi, xj) is the kernel function, both supplied by the user; and the variables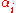
are Lagrange multipliers.
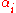, the smallest possible problem involves two such multipliers. Then, for any two multipliers 
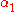and 
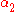, the constraints are reduced to:
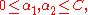
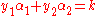
and this reduced problem can be solved analytically.
The algorithm proceeds as follows:
When all the Lagrange multipliers satisfy the KKT conditions (within a user-defined tolerance), the problem has been solved. Although this algorithm is guaranteed to converge, heuristics are used to choose the pair of multipliers so as to accelerate the rate of convergence.
Support vector machine
A support vector machine is a concept in statistics and computer science for a set of related supervised learning methods that analyze data and recognize patterns, used for classification and regression analysis...
s. It was invented by John Platt
John Platt
John Platt is a Principal Researcher in the Machine Learning department at Microsoft Research. Platt has worked for Microsoft since 1997. Prior to Microsoft, Platt had served as Director of Research at Synaptics....
in 1998 at Microsoft Research
Microsoft Research
Microsoft Research is the research division of Microsoft created in 1991 for developing various computer science ideas and integrating them into Microsoft products. It currently employs Turing Award winners C.A.R. Hoare, Butler Lampson, and Charles P...
. SMO is widely used for training support vector machines and is implemented by the popular libsvm tool. The publication of the SMO algorithm in 1998 has generated a lot of excitement in the SVM community, as previously available methods for SVM training were much more complex and required expensive third-party QP
Quadratic programming
Quadratic programming is a special type of mathematical optimization problem. It is the problem of optimizing a quadratic function of several variables subject to linear constraints on these variables....
solvers.
Optimization problem
Consider a binary classificationBinary classification
Binary classification is the task of classifying the members of a given set of objects into two groups on the basis of whether they have some property or not. Some typical binary classification tasks are...
problem with a dataset (x1, y1), ..., (xn, yn), where xi is an input vector and is a binary label corresponding to it. A soft-margin support vector machine
Support vector machine
A support vector machine is a concept in statistics and computer science for a set of related supervised learning methods that analyze data and recognize patterns, used for classification and regression analysis...
is trained by solving a quadratic programming problem, which is expressed in the dual form
Dual problem
In constrained optimization, it is often possible to convert the primal problem to a dual form, which is termed a dual problem. Usually dual problem refers to the Lagrangian dual problem but other dual problems are used, for example, the Wolfe dual problem and the Fenchel dual problem...
as follows:
- subject to:
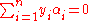
where C is an SVM hyperparameter and K(xi, xj) is the kernel function, both supplied by the user; and the variables
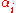are Lagrange multipliers.Algorithm
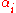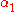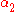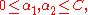
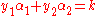
SMO is an iterative algorithm for solving the optimization problem described above. SMO breaks this problem into a series of smallest possible sub-problems, which are then solved analytically. Because of the linear equality constraint involving the Lagrange multipliers, the smallest possible problem involves two such multipliers. Then, for any two multipliers and , the constraints are reduced to:and this reduced problem can be solved analytically.
The algorithm proceeds as follows:
- Find a Lagrange multiplier
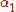that violates the Karush–Kuhn–Tucker (KKT) conditions for the optimization problem. - Pick a second multiplier
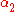and optimize the pair 
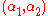. - Repeat steps 1 and 2 until convergence.
When all the Lagrange multipliers satisfy the KKT conditions (within a user-defined tolerance), the problem has been solved. Although this algorithm is guaranteed to converge, heuristics are used to choose the pair of multipliers so as to accelerate the rate of convergence.