Serial module
Encyclopedia
In abstract algebra
, a uniserial module M is a module
over a ring
R, whose submodules are totally ordered
by inclusion. This means simply that for any two submodules N1 and N2 of M, either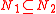
or 
. A module is called a serial module if it is a direct sum of uniserial modules. A ring R is called a right uniserial ring if it is uniserial as a right module over itself, and likewise called a right serial ring if it is a right serial module over itself. Left uniserial and left serial rings are defined in an analogous way, and are in general distinct from their right counterparts.
Any easy motivational example is the quotient ring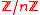
for any integer n>1. This ring is always serial, and is uniserial when n is a prime power
.
The term uniserial has been used differently than the above definition: for clarification see this section.
A partial alphabetical list of important contributors to the theory of serial rings includes the mathematicians Keizo Asano, I. S. Cohen, P.M. Cohn
, Yu. Drozd, D. Eisenbud
, A. Facchini, A.W. Goldie
, Phillip Griffith, I. Kaplansky
, V.V Kirichenko, G. Köthe
, H. Kuppisch, I. Murase, T. Nakayama
, P. Příhoda, G. Puninski, and R. Warfield. References for each author can be found in and .
Following the common ring theoretic convention, if a left/right dependent condition is given without mention of a side (for example, uniserial, serial, Artinian
, Noetherian
) then it is assumed the condition holds on both the left and right. Unless otherwise specified, each ring in this article is a ring with unity, and each module is unital.
and thus is directly indecomposable. It is also easy to see that every finitely generated submodule of M can be generated by a single element, and so M is a Bézout module.
It is known that the endomorphism ring
EndR(M) is a semilocal ring which is very close to a local ring
in the sense that EndR(M) has at most two maximal right ideals. If M is required to be Artinian or Noetherian, then EndR(M) is a local ring.
Since rings with unity always have a maximal right ideal, a right uniserial ring is necessarily local. As noted before, a finitely generated right ideal can be generated by a single element, and so right uniserial rings are right Bézout rings. A right serial ring R necessarily factors in the form
where each ei is an idempotent and eiR is a local, uniserial module. This indicates that R is also a semiperfect ring
, which is a stronger condition than being a semilocal ring.
Köthe showed that the modules of Artinian principal ideal ring
s (which are a special case of serial rings) are direct sums of cyclic submodules. Later, Cohen and Kaplansky determined that a commutative ring R has this property for its modules if and only if R is an Artinian principal ideal ring. Nakayama showed that Artinian serial rings have this property on their modules, and that the converse is not true.
The most general result, perhaps, on the modules of a serial ring is attributed to Drozd and Warfield: it states that every finitely presented module over a serial ring is a direct sum of cyclic uniserial submodules (and hence is serial). If additionally the ring is assumed to be Noetherian, the finitely presented and finitely generated modules coincide, and so all finitely generated modules are serial.
Being right serial is preserved under direct products of rings and modules, and preserved under quotients of rings. Being uniserial is preserved for quotients of rings and modules, but never for products. Being uniserial is preserved for quotients of rings and modules, but never for products. A direct summand of a serial module is not necessarily serial, as was proved by Puninski, but direct summands of finite direct sums of uniserial modules are serial modules .
It has been verified that Jacobson's conjecture holds in Noetherian serial rings.
is trivially uniserial, and likewise semisimple module
s are serial modules.
Many examples of serial rings can be gleaned from the structure sections above. Every valuation ring is a uniserial ring, and all Artinian principal ideal rings are serial rings, as is illustrated by semisimple rings.
More exotic examples include the upper triangular matrices over a division ring Tn(D), and the group ring
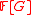for some finite field of prime characteristic p and group G having a cyclic normal p-Sylow subgroup.
where P is some finitely generated projective B module (a progenerator). This is why the results are phrased in terms of indecomposable, basic rings.
In 1975, Kirichenko and Warfield independently and simultaneously published analyses of the structure of Noetherian, non-Artinian serial rings. The results were the same however the methods they used were very different from each other. The study of hereditary
, Noetherian
, prime ring
s, as well as quiver
s defined on serial rings were important tools. The core result states that a right Noetherian, non-Artinian, basic, indecomposable serial ring can be described as a type of matrix ring over a Noetherian, uniserial domain V, whose Jacobson radical J(V) is nonzero. This matrix ring is a subring of Mn(V) for some n, and consists of matrices with entries from V on and above the diagonal, and entries from J(V) below.
Artinian serial ring structure is classified in cases depending on the quiver structure. It turns out that the quiver structure for a basic, indecomposable, Artinian serial ring is always a circle or a line. In the case of the line quiver, the ring is isomorphic to the upper triangular matrices over a division ring (note the similarity to the structure of Noetherian serial rings in the preceding paragraph). A complete description of structure in the case of a circle quiver is beyond the scope of this article, but the complete description can be found in . To paraphrase the result as it appears there: A basic Artinian serial ring whose quiver is a circle is a homomorphic image of a "blow-up" of a basic, indecomposable, serial quasi-Frobenius ring
.
and a monomorphism 
. The dual
notion can be defined: the modules are said to have the same epigeny class, denoted
, if there exists an epimorphism 
and an epimorphism 
.
The following weak form of the Krull-Schmidt theorem holds. Let U1,... Un, V1, ... , Vt be n+t non-zero uniserial right modules over a ring R. Then the direct sums
and 
are isomorphic R-modules if and only if n=t and there exist two permutations 
and 
of 1,2,...,n such that 
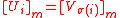and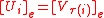 
for every i=1,2,..., n.
This result, due to Facchini, has been extended to infinite direct sums of uniserial modules by Příhoda in 2006. This extension involves the so-called quasismall uniserial modules. These modules were defined by Nguyen Viet Dung and Facchini, and their existence was proved by Puninski. The weak form of the Krull-Schmidt Theorem holds not only for uniserial modules, but also for several other classes of modules (biuniform modules, cyclically presented modules over serial rings, kernels of morphisms between indecomposable injective modules, couniformly presented modules.)
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a uniserial module M is a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R, whose submodules are totally ordered
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
by inclusion. This means simply that for any two submodules N1 and N2 of M, either
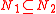or . A module is called a serial module if it is a direct sum of uniserial modules. A ring R is called a right uniserial ring if it is uniserial as a right module over itself, and likewise called a right serial ring if it is a right serial module over itself. Left uniserial and left serial rings are defined in an analogous way, and are in general distinct from their right counterparts.Any easy motivational example is the quotient ring
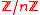for any integer n>1. This ring is always serial, and is uniserial when n is a prime powerPrime power
In mathematics, a prime power is a positive integer power of a prime number.For example: 5=51, 9=32 and 16=24 are prime powers, while6=2×3, 15=3×5 and 36=62=22×32 are not...
.
The term uniserial has been used differently than the above definition: for clarification see this section.
A partial alphabetical list of important contributors to the theory of serial rings includes the mathematicians Keizo Asano, I. S. Cohen, P.M. Cohn
Paul Cohn
Paul Moritz Cohn FRS was Astor Professor of Mathematics at University College London, 1986-9, and author of many textbooks on algebra...
, Yu. Drozd, D. Eisenbud
David Eisenbud
David Eisenbud is an American mathematician. He is a professor of mathematics at the University of California, Berkeley and was Director of the Mathematical Sciences Research Institute from 1997 to 2007....
, A. Facchini, A.W. Goldie
Alfred Goldie
Alfred William Goldie was an English mathematician.Goldie was Assistant Lecturer, Nottingham University 1946-48; Lecturer, then Senior Lecturer, Newcastle University 1948-63; and Professor of Pure Mathematics, Leeds University 1963-86;He won the 1970 Senior Berwick Prize from the London...
, Phillip Griffith, I. Kaplansky
Irving Kaplansky
Irving Kaplansky was a Canadian mathematician.-Biography:He was born in Toronto, Ontario, Canada, after his parents emigrated from Poland and attended the University of Toronto as an undergraduate. After receiving his Ph.D...
, V.V Kirichenko, G. Köthe
Gottfried Köthe
Gottfried Maria Hugo Köthe was an Austrian mathematician working in abstract algebra and functional analysis.- Scientific career :...
, H. Kuppisch, I. Murase, T. Nakayama
Tadashi Nakayama (mathematician)
was a mathematician who made important contributions to representation theory. He received his degrees from Tokyo University and Osaka University and held permanent positions at Osaka University and Nagoya University. He had visiting positions at Princeton University, Illinois University, and...
, P. Příhoda, G. Puninski, and R. Warfield. References for each author can be found in and .
Following the common ring theoretic convention, if a left/right dependent condition is given without mention of a side (for example, uniserial, serial, Artinian
Artinian
In mathematics, Artinian, named for Emil Artin, is an adjective that describes objects that satisfy particular cases of the descending chain condition.*A ring is an Artinian ring if it satisfies the descending chain condition on ideals...
, Noetherian
Noetherian
In mathematics, the adjective Noetherian is used to describe objects that satisfy an ascending or descending chain condition on certain kinds of subobjects; in particular,* Noetherian group, a group that satisfies the ascending chain condition on subgroups...
) then it is assumed the condition holds on both the left and right. Unless otherwise specified, each ring in this article is a ring with unity, and each module is unital.
Properties of uniserial and serial rings and modules
It is immediate that in a uniserial R-module M, all submodules except M and 0 are simultaneously essential and superfluous. If M has a maximal submodule, then M is a local module. M is also clearly a uniform moduleUniform module
In abstract algebra, a module is called a uniform module if the intersection of any two nonzero submodules is nonzero. This is equivalent to saying that every nonzero submodule of M is an essential submodule...
and thus is directly indecomposable. It is also easy to see that every finitely generated submodule of M can be generated by a single element, and so M is a Bézout module.
It is known that the endomorphism ring
Endomorphism ring
In abstract algebra, one associates to certain objects a ring, the object's endomorphism ring, which encodes several internal properties of the object; this may be denoted End...
EndR(M) is a semilocal ring which is very close to a local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
in the sense that EndR(M) has at most two maximal right ideals. If M is required to be Artinian or Noetherian, then EndR(M) is a local ring.
Since rings with unity always have a maximal right ideal, a right uniserial ring is necessarily local. As noted before, a finitely generated right ideal can be generated by a single element, and so right uniserial rings are right Bézout rings. A right serial ring R necessarily factors in the form
where each ei is an idempotent and eiR is a local, uniserial module. This indicates that R is also a semiperfect ringSemiperfect ring
In abstract algebra, a semiperfect ring is a ring over which every finitely generated left module has a projective cover. This property is left right symmetric.- Definition :Let R be ring...
, which is a stronger condition than being a semilocal ring.
Köthe showed that the modules of Artinian principal ideal ring
Principal ideal ring
In mathematics, a principal right ideal ring is a ring R in which every right ideal is of the form xR for some element x of R...
s (which are a special case of serial rings) are direct sums of cyclic submodules. Later, Cohen and Kaplansky determined that a commutative ring R has this property for its modules if and only if R is an Artinian principal ideal ring. Nakayama showed that Artinian serial rings have this property on their modules, and that the converse is not true.
The most general result, perhaps, on the modules of a serial ring is attributed to Drozd and Warfield: it states that every finitely presented module over a serial ring is a direct sum of cyclic uniserial submodules (and hence is serial). If additionally the ring is assumed to be Noetherian, the finitely presented and finitely generated modules coincide, and so all finitely generated modules are serial.
Being right serial is preserved under direct products of rings and modules, and preserved under quotients of rings. Being uniserial is preserved for quotients of rings and modules, but never for products. Being uniserial is preserved for quotients of rings and modules, but never for products. A direct summand of a serial module is not necessarily serial, as was proved by Puninski, but direct summands of finite direct sums of uniserial modules are serial modules .
It has been verified that Jacobson's conjecture holds in Noetherian serial rings.
Examples
Any simple moduleSimple module
In mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
is trivially uniserial, and likewise semisimple module
Semisimple module
In mathematics, especially in the area of abstract algebra known as module theory, a semisimple module or completely reducible module is a type of module that can be understood easily from its parts. A ring which is a semisimple module over itself is known as an artinian semisimple ring...
s are serial modules.
Many examples of serial rings can be gleaned from the structure sections above. Every valuation ring is a uniserial ring, and all Artinian principal ideal rings are serial rings, as is illustrated by semisimple rings.
More exotic examples include the upper triangular matrices over a division ring Tn(D), and the group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
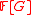for some finite field of prime characteristic p and group G having a cyclic normal p-Sylow subgroup.Structure
This section will deal mainly with Noetherian serial rings and their subclass, Artinian serial rings. In general, rings are first broken down into indecomposable rings. Once the structure of these rings are known, the decomposable rings are direct products of the indecomposable ones. Also, for semiperfect rings such as serial rings, the basic ring is Morita equivalent to the original ring. Thus if R is a serial ring with basic ring B, and the structure of B is known, the theory of Morita equivalence gives that where P is some finitely generated projective B module (a progenerator). This is why the results are phrased in terms of indecomposable, basic rings.In 1975, Kirichenko and Warfield independently and simultaneously published analyses of the structure of Noetherian, non-Artinian serial rings. The results were the same however the methods they used were very different from each other. The study of hereditary
Hereditary ring
In mathematics, especially in the area of abstract algebra known as module theory, a ring R is called hereditary if all submodules of projective modules over R are again projective...
, Noetherian
Noetherian
In mathematics, the adjective Noetherian is used to describe objects that satisfy an ascending or descending chain condition on certain kinds of subobjects; in particular,* Noetherian group, a group that satisfies the ascending chain condition on subgroups...
, prime ring
Prime ring
In abstract algebra, a non-trivial ring R is a prime ring if for any two elements a and b of R, arb = 0 for all r in R implies that either a = 0 or b = 0. Prime ring can also refer to the subring of a field determined by its characteristic...
s, as well as quiver
Quiver (mathematics)
In mathematics, a quiver is a directed graph where loops and multiple arrows between two vertices are allowed, i.e. a multidigraph. They are commonly used in representation theory: a representation, V, of a quiver assigns a vector space V to each vertex x of the quiver and a linear map V to each...
s defined on serial rings were important tools. The core result states that a right Noetherian, non-Artinian, basic, indecomposable serial ring can be described as a type of matrix ring over a Noetherian, uniserial domain V, whose Jacobson radical J(V) is nonzero. This matrix ring is a subring of Mn(V) for some n, and consists of matrices with entries from V on and above the diagonal, and entries from J(V) below.
Artinian serial ring structure is classified in cases depending on the quiver structure. It turns out that the quiver structure for a basic, indecomposable, Artinian serial ring is always a circle or a line. In the case of the line quiver, the ring is isomorphic to the upper triangular matrices over a division ring (note the similarity to the structure of Noetherian serial rings in the preceding paragraph). A complete description of structure in the case of a circle quiver is beyond the scope of this article, but the complete description can be found in . To paraphrase the result as it appears there: A basic Artinian serial ring whose quiver is a circle is a homomorphic image of a "blow-up" of a basic, indecomposable, serial quasi-Frobenius ring
Quasi-Frobenius ring
In ring theory, the class of Frobenius rings and their generalizations are the extension of work done on Frobenius algebras. Perhaps the most important generalization is that of quasi-Frobenius rings , which are in turn generalized by right pseudo-Frobenius rings and right finitely...
.
A decomposition uniqueness property
Two modules U and V are said to have the same monogeny class, denoted [U]m=[V]m, if there exists a monomorphism and a monomorphism . The dualDuality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
notion can be defined: the modules are said to have the same epigeny class, denoted
, if there exists an epimorphism and an epimorphism .The following weak form of the Krull-Schmidt theorem holds. Let U1,... Un, V1, ... , Vt be n+t non-zero uniserial right modules over a ring R. Then the direct sums
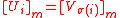and are isomorphic R-modules if and only if n=t and there exist two permutations and of 1,2,...,n such that and 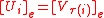for every i=1,2,..., n.This result, due to Facchini, has been extended to infinite direct sums of uniserial modules by Příhoda in 2006. This extension involves the so-called quasismall uniserial modules. These modules were defined by Nguyen Viet Dung and Facchini, and their existence was proved by Puninski. The weak form of the Krull-Schmidt Theorem holds not only for uniserial modules, but also for several other classes of modules (biuniform modules, cyclically presented modules over serial rings, kernels of morphisms between indecomposable injective modules, couniformly presented modules.)