Set theory of the real line
Encyclopedia
Set theory of the real line is an area of mathematics
concerned with the application of set theory
to aspects of the real numbers.
For example, one knows that all countable sets of reals are null
, i.e. have Lebesgue measure
0; one might therefore ask the least possible size of a set
which is not Lebesgue null. This invariant is called the uniformity of the ideal
of null sets, denoted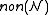
. There are many such invariants associated with this and other ideals, e.g. the ideal of meagre
sets, plus more which do not have a characterisation in terms of ideals. If the continuum hypothesis
(CH) holds, then all such invariants are equal to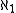
, the least uncountable cardinal
. For example, we know
is uncountable, but being the size of some set of reals under CH it can be at most 
.
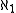On the other hand, if one assumes Martin's Axiom
(MA) all common invariants are "big", that is equal to
, the cardinality of the continuum
. Martin's Axiom is consistent with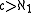
. In fact one should view Martin's Axiom as a forcing
axiom that negates the need to do specific forcings of a certain class (those satisfying the ccc
, since the consistency of MA with large continuum is proved by doing all such forcings (up to a certain size shown to be sufficient). Each invariant can be made large by some ccc forcing, thus each is big given MA.
If one restricts to specific forcings, some invariants will become big while others remain small. Analysing these effects is the major work of the area, seeking to determine which inequalities between invariants are provable and which are inconsistent with ZFC. The inequalities among the ideals of measure
(null sets) and category
(meagre sets) are captured in Cichon's diagram. Seventeen models (forcing constructions) were produced during the 1980s, starting with work of Arnold Miller, to demonstrate that no other inequalities are provable. These are analysed in detail in the book by Tomek Bartoszynski and Haim Judah, two of the eminent workers in the field.
One curious result is that if you can cover the real line with
meagre sets (where 
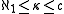) then 
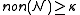; conversely if you can cover the real line with 
null sets then the least non-meagre set has size at least 
; both of these results follow from the existence of a decomposition of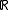 
as the union of a meagre set and a null set.
One of the last great unsolved problems of the area was the consistency of
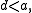
proved in 1998 by Saharon Shelah
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
concerned with the application of set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
to aspects of the real numbers.
For example, one knows that all countable sets of reals are null
Null set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
, i.e. have Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
0; one might therefore ask the least possible size of a set
which is not Lebesgue null. This invariant is called the uniformity of the ideal
Ideal (set theory)
In the mathematical field of set theory, an ideal is a collection of sets that are considered to be "small" or "negligible". Every subset of an element of the ideal must also be in the ideal , and the union of any two elements of the ideal must also be in the ideal.More formally, given a set X, an...
of null sets, denoted
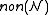. There are many such invariants associated with this and other ideals, e.g. the ideal of meagreMeagre set
In the mathematical fields of general topology and descriptive set theory, a meagre set is a set that, considered as a subset of a topological space, is in a precise sense small or negligible...
sets, plus more which do not have a characterisation in terms of ideals. If the continuum hypothesis
Continuum hypothesis
In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
(CH) holds, then all such invariants are equal to
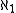, the least uncountable cardinalCardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
. For example, we know
is uncountable, but being the size of some set of reals under CH it can be at most 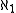.On the other hand, if one assumes Martin's Axiom
Martin's axiom
In the mathematical field of set theory, Martin's axiom, introduced by , is a statement which is independent of the usual axioms of ZFC set theory. It is implied by the continuum hypothesis, so certainly consistent with ZFC, but is also known to be consistent with ZF + ¬ CH...
(MA) all common invariants are "big", that is equal to
, the cardinality of the continuumCardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
. Martin's Axiom is consistent with
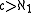. In fact one should view Martin's Axiom as a forcingForcing (mathematics)
In the mathematical discipline of set theory, forcing is a technique invented by Paul Cohen for proving consistency and independence results. It was first used, in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory...
axiom that negates the need to do specific forcings of a certain class (those satisfying the ccc
Countable chain condition
In order theory, a partially ordered set X is said to satisfy the countable chain condition, or to be ccc, if every strong antichain in X is countable. There are really two conditions: the upwards and downwards countable chain conditions. These are not equivalent...
, since the consistency of MA with large continuum is proved by doing all such forcings (up to a certain size shown to be sufficient). Each invariant can be made large by some ccc forcing, thus each is big given MA.
If one restricts to specific forcings, some invariants will become big while others remain small. Analysing these effects is the major work of the area, seeking to determine which inequalities between invariants are provable and which are inconsistent with ZFC. The inequalities among the ideals of measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
(null sets) and category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
(meagre sets) are captured in Cichon's diagram. Seventeen models (forcing constructions) were produced during the 1980s, starting with work of Arnold Miller, to demonstrate that no other inequalities are provable. These are analysed in detail in the book by Tomek Bartoszynski and Haim Judah, two of the eminent workers in the field.
One curious result is that if you can cover the real line with
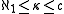meagre sets (where ) then 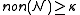; conversely if you can cover the real line with null sets then the least non-meagre set has size at least ; both of these results follow from the existence of a decomposition of 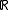as the union of a meagre set and a null set.One of the last great unsolved problems of the area was the consistency of
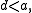
proved in 1998 by Saharon Shelah
Saharon Shelah
Saharon Shelah is an Israeli mathematician. He is a professor of mathematics at the Hebrew University of Jerusalem and Rutgers University in New Jersey.-Biography:...
.