
Seven dimensional cross product
Encyclopedia
In mathematics
, the seven-dimensional cross product is a bilinear operation on vectors in a seven-dimensional space
. It assigns to any two vectors a, b in ℝ7 a vector a × b ∈ ℝ7. In seven dimensions there also exists a cross product involving six vectors (which is linear but not binary), discussed briefly in the section on generalizations.
As in the more familiar three-dimensional cross product
, the binary cross product in seven dimensions is alternating and orthogonal to the original vectors, but unlike that case, however, it does not satisfy the Jacobi identity
. The seven dimensional cross product has the same relationship to octonion
s as the three-dimensional cross product does to quaternion
s, and apart from the trivial cases of zero and one dimensions, binary cross products can be shown to exist only in three and seven dimensions.
Entries in the interior give the product of the corresponding vectors on the left and the top in that order (the product is anti-commutative). Some entries are highlighted to emphasize the symmetry.
The table can be summarized by the relation
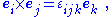
where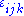 is a completely antisymmetric tensor with a positive value +1 when ijk = 123, 145, 176, 246, 257, 347, 365. By picking out the factors leading to the unit vector e1, for example, one finds the formula for the e1 component of x × y. Namely
is a completely antisymmetric tensor with a positive value +1 when ijk = 123, 145, 176, 246, 257, 347, 365. By picking out the factors leading to the unit vector e1, for example, one finds the formula for the e1 component of x × y. Namely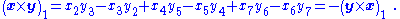
The top left 3 × 3 corner of the table is the same as the cross product in three dimensions. It also may be noticed that orthogonality of the cross product to its constituents x and y is a requirement upon the entries in this table. However, because of the many possible multiplication tables, general results for the cross product are best developed using a basis-independent formulation, as introduced next.
V as a bilinear map from V × V to V mapping vectors x and y in V to another vector x × y also in V, where x × y has the properties
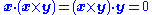 (orthogonality),
(orthogonality),
and:
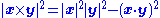 (magnitude),
(magnitude),
where (x·y) is the Euclidean dot product
and |x| is the vector norm
. The first property states that the cross product is perpendicular to its arguments, while the second property gives the magnitude of the cross product. An equivalent expression in terms of the angle
θ between the vectors is
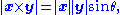
or the area of the parallelogram
in the plane of x and y with the two vectors as sides. As a third alternative the following can be shown to be equivalent to either expression for the magnitude:
The restriction to 0, 1, 3 and 7 dimensions is related to Hurwitz's theorem, that normed division algebra
s are only possible in 1, 2, 4 and 8 dimensions. The cross product is derived from the product of the algebra by considering the product restricted to the 0, 1, 3, or 7 imaginary dimensions of the algebra. Again discarding trivial products the product can only be defined this way in three and seven dimensions.
In contrast with three dimensions where the cross product is unique (apart from sign), there are many possible binary cross products in seven dimensions. One way to see this is to note that given any pair of vectors x and y ∈ ℝ7 and any vector v of magnitude |v| = |x||y| sinθ in the five dimensional space perpendicular to the plane spanned by x and y, it is possible to find a cross product with a multiplication table (and an associated set of basis vectors) such that x × y = v. That leaves open the question of just how many vector pairs like x and y can be matched to specified directions like v before the limitations of any particular table intervene.
Another difference between the three dimensional cross product and a seven dimensional cross product is:
This statement is exemplified by every multiplication table, because any specific unit vector selected as a product occurs as a mapping from three different pairs of unit vectors, once with a plus sign and once with a minus sign. Each of these different pairs, of course, corresponds to another plane being mapped into the same direction.
Further properties follow from the definition, including the following identities:
 (anticommutativity
(anticommutativity
),
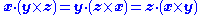 (scalar triple product),
(scalar triple product),
 (Malcev identity
(Malcev identity
),
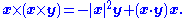
Other properties follow only in the three dimensional case, and are not satisfied by the seven dimensional cross product, notably,
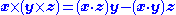 (vector triple product),
(vector triple product),
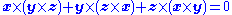 (Jacobi identity
(Jacobi identity
).
{ej} may be selected and a multiplication table provided that determines all the products {ei× ej}. One possible multiplication table is described in the Example section, but it is not unique. Unlike three dimensions, there are many tables because every pair of unit vectors is perpendicular to five other unit vectors, allowing many choices for each cross product.
Once we have established a multiplication table, it is then applied to general vectors x and y by expressing x and y in terms of the basis and expanding x×y through bilinearity.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the seven-dimensional cross product is a bilinear operation on vectors in a seven-dimensional space
Seven-dimensional space
In physics and mathematics, a sequence of n numbers can also be understood as a location in n-dimensional space. When n = 7, the set of all such locations is called 7-dimensional Euclidean space...
. It assigns to any two vectors a, b in ℝ7 a vector a × b ∈ ℝ7. In seven dimensions there also exists a cross product involving six vectors (which is linear but not binary), discussed briefly in the section on generalizations.
As in the more familiar three-dimensional cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
, the binary cross product in seven dimensions is alternating and orthogonal to the original vectors, but unlike that case, however, it does not satisfy the Jacobi identity
Jacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
. The seven dimensional cross product has the same relationship to octonion
Octonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s as the three-dimensional cross product does to quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s, and apart from the trivial cases of zero and one dimensions, binary cross products can be shown to exist only in three and seven dimensions.
Example
The postulates underlying construction of the seven-dimensional cross product are presented in the section Definition. As context for that discussion, the historically first example of the cross product is tabulated below using e1 to e7 as basis vectors. This table is one of 480 independent multiplication tables fitting the pattern that each unit vector appears once in each column and once in each row. Thus, each unit vector appears as a product in the table six times, three times with a positive sign and three with a negative sign because of antisymmetry about the diagonal of zero entries. For example, e1 = e2 × e3 = e4 × e5 = e7 × e6 and the negative entries are the reversed cross-products.| bgcolor=| |
>- | | |
>- | | |
>- |
| | bgcolor=white | | >bgcolor=#D3D3D3 | | >- | | bgcolor=#D3D3D3 | | >bgcolor=#D3D3D3 | | |
|---|---|---|---|---|---|
| | bgcolor=#D3D3D3 | | |||||
| >bgcolor=#D3D3D3 | | >bgcolor=#D3D3D3 | | > bgcolor=#D3D3D3 | | |||
| |bgcolor=#D3D3D3 | | > bgcolor=#D3D3D3 | | ||||
| > bgcolor=#D3D3D3 | | |||||
Entries in the interior give the product of the corresponding vectors on the left and the top in that order (the product is anti-commutative). Some entries are highlighted to emphasize the symmetry.
The table can be summarized by the relation
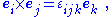
where
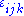 is a completely antisymmetric tensor with a positive value +1 when ijk = 123, 145, 176, 246, 257, 347, 365. By picking out the factors leading to the unit vector e1, for example, one finds the formula for the e1 component of x × y. Namely
is a completely antisymmetric tensor with a positive value +1 when ijk = 123, 145, 176, 246, 257, 347, 365. By picking out the factors leading to the unit vector e1, for example, one finds the formula for the e1 component of x × y. Namely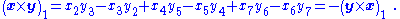
The top left 3 × 3 corner of the table is the same as the cross product in three dimensions. It also may be noticed that orthogonality of the cross product to its constituents x and y is a requirement upon the entries in this table. However, because of the many possible multiplication tables, general results for the cross product are best developed using a basis-independent formulation, as introduced next.
Definition
We can define a cross product on a Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
V as a bilinear map from V × V to V mapping vectors x and y in V to another vector x × y also in V, where x × y has the properties
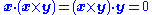 (orthogonality),
(orthogonality),and:
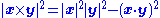 (magnitude),
(magnitude),where (x·y) is the Euclidean dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
and |x| is the vector norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
. The first property states that the cross product is perpendicular to its arguments, while the second property gives the magnitude of the cross product. An equivalent expression in terms of the angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
θ between the vectors is
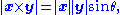
or the area of the parallelogram
Parallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
in the plane of x and y with the two vectors as sides. As a third alternative the following can be shown to be equivalent to either expression for the magnitude:
Consequences of the defining properties
Given the three basic properties of (i) bilinearity, (ii) orthogonality and (iii) magnitude discussed in the section on definition, a nontrivial cross product exists only in three and seven dimensions. This restriction upon dimensionality can be shown by postulating the properties required for the cross product, then deducing a equation which is only satisfied when the dimension is 0, 1, 3 or 7. In zero dimensions there is only the zero vector, while in one dimension all vectors are parallel, so in both these cases a cross product must be identically zero.The restriction to 0, 1, 3 and 7 dimensions is related to Hurwitz's theorem, that normed division algebra
Normed division algebra
In mathematics, a normed division algebra A is a division algebra over the real or complex numbers which is also a normed vector space, with norm || · || satisfying the following property:\|xy\| = \|x\| \|y\| for all x and y in A....
s are only possible in 1, 2, 4 and 8 dimensions. The cross product is derived from the product of the algebra by considering the product restricted to the 0, 1, 3, or 7 imaginary dimensions of the algebra. Again discarding trivial products the product can only be defined this way in three and seven dimensions.
In contrast with three dimensions where the cross product is unique (apart from sign), there are many possible binary cross products in seven dimensions. One way to see this is to note that given any pair of vectors x and y ∈ ℝ7 and any vector v of magnitude |v| = |x||y| sinθ in the five dimensional space perpendicular to the plane spanned by x and y, it is possible to find a cross product with a multiplication table (and an associated set of basis vectors) such that x × y = v. That leaves open the question of just how many vector pairs like x and y can be matched to specified directions like v before the limitations of any particular table intervene.
Another difference between the three dimensional cross product and a seven dimensional cross product is:
This statement is exemplified by every multiplication table, because any specific unit vector selected as a product occurs as a mapping from three different pairs of unit vectors, once with a plus sign and once with a minus sign. Each of these different pairs, of course, corresponds to another plane being mapped into the same direction.
Further properties follow from the definition, including the following identities:
 (anticommutativity
(anticommutativityAnticommutativity
In mathematics, anticommutativity is the property of an operation that swapping the position of any two arguments negates the result. Anticommutative operations are widely used in algebra, geometry, mathematical analysis and, as a consequence, in physics: they are often called antisymmetric...
),
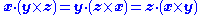 (scalar triple product),
(scalar triple product), (Malcev identity
(Malcev identityMalcev algebra
In mathematics, a Malcev algebra over a field is a nonassociative algebra that is antisymmetric, so thatxy = -yx\ and satisfies the Malcev identity = x + x + y.\...
),
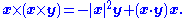
Other properties follow only in the three dimensional case, and are not satisfied by the seven dimensional cross product, notably,
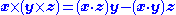 (vector triple product),
(vector triple product),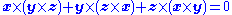 (Jacobi identity
(Jacobi identityJacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
).
Coordinate expressions
To define a particular cross product, an orthonormal basisOrthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
{ej} may be selected and a multiplication table provided that determines all the products {ei× ej}. One possible multiplication table is described in the Example section, but it is not unique. Unlike three dimensions, there are many tables because every pair of unit vectors is perpendicular to five other unit vectors, allowing many choices for each cross product.
Once we have established a multiplication table, it is then applied to general vectors x and y by expressing x and y in terms of the basis and expanding x×y through bilinearity.
| | bgcolor=white | | >bgcolor=#D3D3D3 | | | bgcolor=#f9f9f9 | | |||
|---|---|---|---|---|---|
| | bgcolor=#D3D3D3 | | > bgcolor=#D3D3D3 | | ||||
| >bgcolor=#D3D3D3 | | > bgcolor=white | | > bgcolor=#D3D3D3 | | > bgcolor=#D3D3D3 | | ||
| >bgcolor=#D3D3D3 | | > bgcolor=#D3D3D3 | | ||||
| | bgcolor=#D3D3D3 | | > bgcolor=#D3D3D3 | | ||||


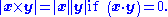
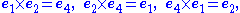
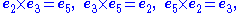
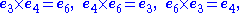

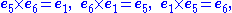
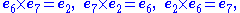
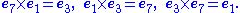
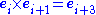

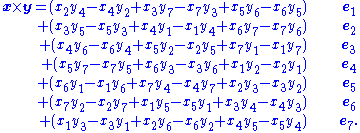
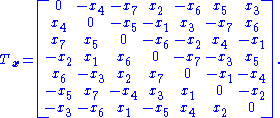
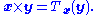
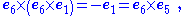
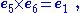
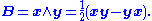
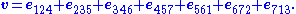
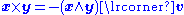
 is the left contraction operator from geometric algebra.
is the left contraction operator from geometric algebra.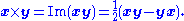

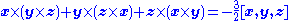
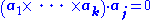 (orthogonality)
(orthogonality) (Gram determinant)
(Gram determinant)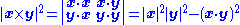 ,
,