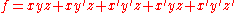Shannon expansion
Encyclopedia
In mathematics, Shannon's expansion or the Shannon decomposition is a method by which a Boolean function can be represented by the sum of two sub-functions of the original. Although it is often credited to Claude Shannon, Boole proved this much earlier. Shannon is credited with many other important aspects of Boolean algebra.
:
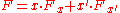
where
is any function and 
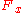and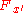 
are positive and negative Shannon cofactors of 
, respectively. A positive Shannon cofactor of function 
with respect to variable 
is defined as that function with all 
’s set to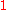 
. A negative Shannon cofactor is the same, but sets all 
’s to 
.
The Shannon expansion theorem is an important idea in Boolean algebra. It paved the way for Binary decision diagram
s, Satisfiability solvers
, and many other techniques relevant for computer engineering
and formal verification
of digital circuits.
As presented in Jan.1948 paper, "The Synthesis of Two-Terminal Switching Circuits" . Simply stated as the expansion of a function as:
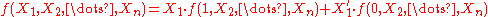
followed by the expansion for two variables, and noting that expansion can be continued for any number of variables.
Now, notice that you can re-write the function in terms of any two variables
— namely, a variable and its complement. Observe:
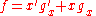
Now, to make the final expression equivalent to our composition of functions, simply apply the distributive theorem to the function about x:
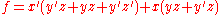
Now we have expanded the function f about the variable x.
In Boolean algebra, you can AND any literal or term with 1, and still achieve the same truth value. With that in mind, let's look at this function:
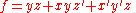
If we desire to expand around the variable x, we simply don't have enough information in the first term to accomplish this task. So, what do we do? Remember what was said above: AND the literal with 1, or, in this case
.
Expand:
This function contains the variable about which we want to expand the expression, so now we should have no problem performing the expansion:
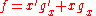
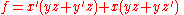
The expansion is complete.
Of course, you can perform Shannon's Expansion about any variable you desire, so long as you can provide for that variable in the expression without changing the truth value of the expression. Also, you can perform multiple expansions of a single function (e.g. about x, then about y) or, you can even perform the expansion about many variables at once (e.g. about xy). The result is a functionally equivalent expression for the variables involved.
Why make an expression larger? Is Boolean algebra all about minimizing functions?
Consider a logic device called a multiplexer
. Multiplexers take n select inputs, and 2n data inputs, and give one output. Once you expand any boolean function about any number of variables, you can use the variables that the function was expanded about as the select inputs, and their respective composed functions as the corresponding data inputs.
Expansion
The Shannon expansion develops the idea that Boolean functions can be reduced by means of the identityIdentity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
:
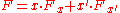
where
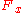is any function and and 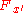are positive and negative Shannon cofactors of , respectively. A positive Shannon cofactor of function with respect to variable is defined as that function with all ’s set to 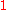. A negative Shannon cofactor is the same, but sets all ’s to .The Shannon expansion theorem is an important idea in Boolean algebra. It paved the way for Binary decision diagram
Binary decision diagram
In the field of computer science, a binary decision diagram or branching program, like a negation normal form or a propositional directed acyclic graph , is a data structure that is used to represent a Boolean function. On a more abstract level, BDDs can be considered as a compressed...
s, Satisfiability solvers
Boolean satisfiability problem
In computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
, and many other techniques relevant for computer engineering
Computer engineering
Computer engineering, also called computer systems engineering, is a discipline that integrates several fields of electrical engineering and computer science required to develop computer systems. Computer engineers usually have training in electronic engineering, software design, and...
and formal verification
Formal verification
In the context of hardware and software systems, formal verification is the act of proving or disproving the correctness of intended algorithms underlying a system with respect to a certain formal specification or property, using formal methods of mathematics .- Usage :Formal verification can be...
of digital circuits.
As presented in Jan.1948 paper, "The Synthesis of Two-Terminal Switching Circuits" . Simply stated as the expansion of a function as:
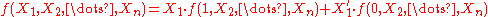
followed by the expansion for two variables, and noting that expansion can be continued for any number of variables.
Example
Take this as our function:
Now, notice that you can re-write the function in terms of any two variables
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
— namely, a variable and its complement. Observe:
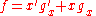
Now, to make the final expression equivalent to our composition of functions, simply apply the distributive theorem to the function about x:
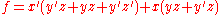
Now we have expanded the function f about the variable x.
x Variables
In Shannon's expansion the term x is very significant but problems can arise in simple equations. What if there were no x variable in one or more of the terms? Problems here can lead to confusion. Dealing with no x variable in one or more of the terms can be simple. The solution is not always intuitive.In Boolean algebra, you can AND any literal or term with 1, and still achieve the same truth value. With that in mind, let's look at this function:
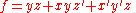
If we desire to expand around the variable x, we simply don't have enough information in the first term to accomplish this task. So, what do we do? Remember what was said above: AND the literal with 1, or, in this case
.Expand:
This function contains the variable about which we want to expand the expression, so now we should have no problem performing the expansion:
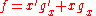
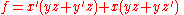
The expansion is complete.
Of course, you can perform Shannon's Expansion about any variable you desire, so long as you can provide for that variable in the expression without changing the truth value of the expression. Also, you can perform multiple expansions of a single function (e.g. about x, then about y) or, you can even perform the expansion about many variables at once (e.g. about xy). The result is a functionally equivalent expression for the variables involved.
Expanding and minimizing
- You can expand a function
- You can minimize a function
Why make an expression larger? Is Boolean algebra all about minimizing functions?
Consider a logic device called a multiplexer
Multiplexer
In electronics, a multiplexer is a device that selects one of several analog or digital input signals and forwards the selected input into a single line. A multiplexer of 2n inputs has n select lines, which are used to select which input line to send to the output...
. Multiplexers take n select inputs, and 2n data inputs, and give one output. Once you expand any boolean function about any number of variables, you can use the variables that the function was expanded about as the select inputs, and their respective composed functions as the corresponding data inputs.
External links
- Shannon’s Decomposition Example with multiplexers.
- Optimizing Sequential Cycles Through Shannon Decomposition and Retiming (PDF) Paper on application.