Shift space
Encyclopedia
In symbolic dynamics
and related branches of mathematics
, a shift space or subshift is a set of infinite
word
s representing the evolution of a discrete system
. In fact, shift spaces and symbolic dynamical systems
are often considered synonym
s.
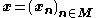, where 
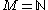(resp. 
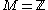) and 
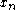is in A for any integer n.
The shift operator
acts on an infinite or bi-infinite word by shifting all symbols to the left, i.e.,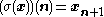
for all n.
In the following we choose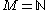
and thus speak of infinite words, but all definitions are naturally generalizable to the bi-infinite case.
with respect to the natural product topology
of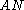
and invariant under the shift operator. Thus a set 
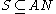is a subshift if and only if
A shift space S is sometimes denoted as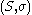
to emphasize the role of the shift operator.
Some authors use the term subshift for a set of infinite words that is just invariant under the shift, and reserve the term shift space for those which are also closed.
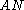is a shift space if and only if there exists a set X of finite word
s such that S coincides with the set of all infinite words over A having no factor
in X.
When X is a regular language
, the corresponding subshift is called sofic. In particular, if X is finite then S is called a subshift of finite type
.
.
Let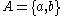
. The set of all infinite words over A containing at most one b is a sofic subshift, not of finite type.
Symbolic dynamics
In mathematics, symbolic dynamics is the practice of modeling a topological or smooth dynamical system by a discrete space consisting of infinite sequences of abstract symbols, each of which corresponds to a state of the system, with the dynamics given by the shift operator...
and related branches of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a shift space or subshift is a set of infinite
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
word
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
s representing the evolution of a discrete system
Discrete system
A discrete system is a system with a countable number of states. Discrete systems may be contrasted with continuous systems, which may also be called analog systems. A final discrete system is often modeled with a directed graph and is analyzed for correctness and complexity according to...
. In fact, shift spaces and symbolic dynamical systems
Symbolic dynamics
In mathematics, symbolic dynamics is the practice of modeling a topological or smooth dynamical system by a discrete space consisting of infinite sequences of abstract symbols, each of which corresponds to a state of the system, with the dynamics given by the shift operator...
are often considered synonym
Synonym
Synonyms are different words with almost identical or similar meanings. Words that are synonyms are said to be synonymous, and the state of being a synonym is called synonymy. The word comes from Ancient Greek syn and onoma . The words car and automobile are synonyms...
s.
Notation
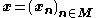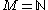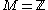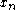Let A be a finite set of states. An infinite (respectively bi-infinite) word over A is a sequence, where (resp. ) and is in A for any integer n.The shift operator
Shift operator
In mathematics, and in particular functional analysis, the shift operator or translation operator is an operator that takes a function to its translation . In time series analysis, the shift operator is called the lag operator....
acts on an infinite or bi-infinite word by shifting all symbols to the left, i.e.,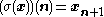 for all n.In the following we choose
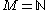and thus speak of infinite words, but all definitions are naturally generalizable to the bi-infinite case.Definition
A set of infinite words over A is a shift space if it is closedClosed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
with respect to the natural product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
of
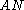and invariant under the shift operator. Thus a set 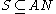is a subshift if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
- for any (pointwisePointwise convergenceIn mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
) convergent sequence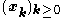
of elements of S, the limitLimit of a sequenceThe limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
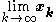also belongs to S; and -
.
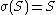A shift space S is sometimes denoted as
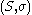to emphasize the role of the shift operator.Some authors use the term subshift for a set of infinite words that is just invariant under the shift, and reserve the term shift space for those which are also closed.
Characterization and sofic subshifts
A subset S of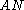 is a shift space if and only if there exists a set X of finite wordString (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
s such that S coincides with the set of all infinite words over A having no factor
Substring
A subsequence, substring, prefix or suffix of a string is a subset of the symbols in a string, where the order of the elements is preserved...
in X.
When X is a regular language
Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
, the corresponding subshift is called sofic. In particular, if X is finite then S is called a subshift of finite type
Subshift of finite type
In mathematics, subshifts of finite type are used to model dynamical systems, and in particular are the objects of study in symbolic dynamics and ergodic theory. They also describe the set of all possible sequences executed by a finite state machine...
.
Examples
The first trivial example of shift space (of finite type) is the full shift.Let
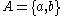. The set of all infinite words over A containing at most one b is a sofic subshift, not of finite type.