Shilov boundary
Encyclopedia
In functional analysis
, a branch of mathematics, the Shilov boundary is the smallest closed
subset of the structure space
of a commutative Banach algebra
where an analog of the maximum modulus principle
holds. It is named after its discoverer, Georgii Evgen'evich Shilov
.
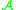be a commutative Banach algebra
and let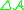
be its structure space
equipped with the relative weak*-topology
of the dual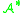
. A closed (in this topology) subset 
of 
is called a boundary o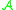f 
if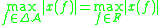 
for all 
.
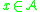The set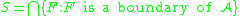
is called the Shilov boundary. It has been proved by Shilov that 
is a boundary of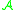 
.
Thus one may also say that Shilov boundary is the unique set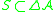
which satisfies
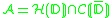be the disc algebra, i.e. the functions holomorphic in 
and continuous
in the closure
of
with supremum norm and usual algebraic operations. Then 
and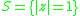 
.
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, a branch of mathematics, the Shilov boundary is the smallest closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
subset of the structure space
Structure space
The structure space of a commutative Banach algebra is an analog of the spectrum of a C*-algebra. It consists of all multiplicative linear functionals on the algebra. The Gelfand representation of the Banach algebra is a map taking the Banach algebra elements to continuous functions on the...
of a commutative Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
where an analog of the maximum modulus principle
Maximum modulus principle
In mathematics, the maximum modulus principle in complex analysis states that if f is a holomorphic function, then the modulus |f| cannot exhibit a true local maximum that is properly within the domain of f....
holds. It is named after its discoverer, Georgii Evgen'evich Shilov
Georgii Evgen'evich Shilov
Georgi Evgen'evich Shilov was a Soviet mathematician and expert in the field of functional analysis, who contributed to the theory of normed rings and generalized functions....
.
Precise definition and existence
Let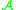 be a commutative Banach algebraBanach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
and let
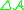be its structure spaceStructure space
The structure space of a commutative Banach algebra is an analog of the spectrum of a C*-algebra. It consists of all multiplicative linear functionals on the algebra. The Gelfand representation of the Banach algebra is a map taking the Banach algebra elements to continuous functions on the...
equipped with the relative weak*-topology
Weak topology
In mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
of the dual
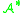. A closed (in this topology) subset of is called a boundary o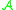f if 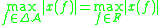for all 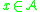.The set
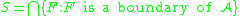is called the Shilov boundary. It has been proved by Shilov that is a boundary of 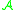.Thus one may also say that Shilov boundary is the unique set
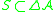which satisfies
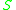is a boundary of 
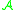, and- whenever
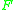is a boundary of 
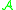, then 
.
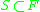Examples
- Let
be the open unit disc in the complex planeComplex planeIn mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
and let
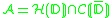be the disc algebra, i.e. the functions holomorphic in and continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
in the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of
with supremum norm and usual algebraic operations. Then and 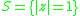.