
Siegel's lemma
Encyclopedia
In transcendental
number theory
and Diophantine approximation
, Siegel's lemma refers to bounds on the solutions of linear equations obtained by the construction of auxiliary function
s. The existence of these polynomials was proven by Axel Thue
; Thue's proof used Dirichlet's box principle. Carl Ludwig Siegel
published his lemma in 1929. It is a pure existence theorem
for a system of linear equations.
Siegel's lemma has been refined in recent years to produce sharper bounds on the estimates given by the lemma.
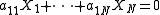


where the coefficients are rational integers, not all 0, and bounded by B. The system then has a solution
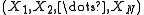
with the Xs all rational integers, not all 0, and bounded by

gave the following sharper bound for the Xs: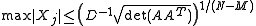
where D is the greatest common divisor of the M by M minors of the matrix A, and AT is its transpose.
Their proof involved replacing the Dirichlet box principle by techniques from the geometry of numbers
.
Transcendence theory
Transcendence theory is a branch of number theory that investigates transcendental numbers, in both qualitative and quantitative ways.-Transcendence:...
number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
and Diophantine approximation
Diophantine approximation
In number theory, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real numbers by rational numbers....
, Siegel's lemma refers to bounds on the solutions of linear equations obtained by the construction of auxiliary function
Auxiliary function
In mathematics, auxiliary functions are an important construction in transcendental number theory. They are functions that appear in most proofs in this area of mathematics and that have specific, desirable properties, such as taking the value zero for many arguments, or having a zero of high...
s. The existence of these polynomials was proven by Axel Thue
Axel Thue
Axel Thue was a Norwegian mathematician, known for highly original work in diophantine approximation, and combinatorics....
; Thue's proof used Dirichlet's box principle. Carl Ludwig Siegel
Carl Ludwig Siegel
Carl Ludwig Siegel was a mathematician specialising in number theory and celestial mechanics. He was one of the most important mathematicians of the 20th century.-Biography:...
published his lemma in 1929. It is a pure existence theorem
Existence theorem
In mathematics, an existence theorem is a theorem with a statement beginning 'there exist ..', or more generally 'for all x, y, ... there exist ...'. That is, in more formal terms of symbolic logic, it is a theorem with a statement involving the existential quantifier. Many such theorems will not...
for a system of linear equations.
Siegel's lemma has been refined in recent years to produce sharper bounds on the estimates given by the lemma.
Statement
Suppose we are given a system of M linear equations in N unknowns such that N > M, say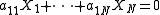


where the coefficients are rational integers, not all 0, and bounded by B. The system then has a solution
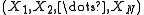
with the Xs all rational integers, not all 0, and bounded by

gave the following sharper bound for the Xs:
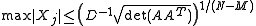
where D is the greatest common divisor of the M by M minors of the matrix A, and AT is its transpose.
Their proof involved replacing the Dirichlet box principle by techniques from the geometry of numbers
Geometry of numbers
In number theory, the geometry of numbers studies convex bodies and integer vectors in n-dimensional space. The geometry of numbers was initiated by ....
.

