Signature (topology)
Encyclopedia
In the mathematical
field of topology
, the signature is an integer invariant
which is defined for an oriented manifold
M of dimension d=4k divisible by four (doubly even-dimensional).
This invariant of a manifold has been studied in detail, starting with Rokhlin's theorem
for 4-manifolds.
and orientable manifold M of dimension 4k, the cup product
gives rise to a quadratic form
Q on the 'middle' real cohomology group
The basic identity for the cup product
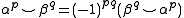
shows that with p = q = 2k the product is symmetric. It takes values in
If we assume also that M is compact, Poincaré duality
identifies this with
which can be identified with Z. Therefore cup product, under these hypotheses, does give rise to a symmetric bilinear form
on H2k(M,Z); and therefore to a quadratic form Q. The form Q is non-degenerate due to Poincaré duality, as it pairs non-degenerately with itself. More generally, the signature can be defined in this way for any general compact polyhedron
with 4n-dimensional Poincaré duality.
The signature of M is by definition the signature of Q. If M is not connected, its signature is defined to be the sum of the signatures of its connected components.
: the signature can be interpreted as the 4k-dimensional (simply-connected) symmetric L-group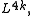
or as the 4k-dimensional quadratic L-group 
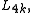and these invariants do not always vanish for other dimensions. The Kervaire invariant is a mod 2 (i.e., an element of 
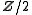) for framed manifolds of dimension 4k+2 (the quadratic L-group 
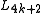), while the de Rham invariant is a mod 2 invariant of manifolds of dimension 4k+1 (the symmetric L-group 
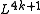); the other dimensional L-groups vanish.
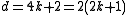is twice an odd integer (singly even), the same construction gives rise to an antisymmetric bilinear form. Such forms do not have a signature invariant; if they are non-degenerate, any two such forms are equivalent. However, if one takes a quadratic refinement of the form, which occurs if one has a framed manifold, then the resulting ε-quadratic forms need not be equivalent, being distinguished by the Arf invariant
. The resulting invariant of a manifold is called the Kervaire invariant.
(1954) showed that the signature of a manifold is a cobordism invariant, and in particular is given by some linear combination of its Pontryagin
numbers. Friedrich Hirzebruch
(1954) found an explicit expression for this linear combination as the L genus of the manifold. William Browder
(1962) proved that a simply-connected compact polyhedron
with 4n-dimensional Poincaré duality
is homotopy equivalent to a manifold if and only if its signature satisfies the expression of the Hirzebruch signature theorem.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, the signature is an integer invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
which is defined for an oriented manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
M of dimension d=4k divisible by four (doubly even-dimensional).
This invariant of a manifold has been studied in detail, starting with Rokhlin's theorem
Rokhlin's theorem
In 4-dimensional topology, a branch of mathematics, Rokhlin's theorem states that if a smooth, compact 4-manifold M has a spin structure , then the signature of its intersection form, a quadratic form on the second cohomology group H2, is divisible by 16...
for 4-manifolds.
Definition
Given a connectedConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
and orientable manifold M of dimension 4k, the cup product
Cup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
gives rise to a quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
Q on the 'middle' real cohomology group
- H2k(M,Z).
The basic identity for the cup product
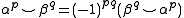
shows that with p = q = 2k the product is symmetric. It takes values in
- H4k(M,Z).
If we assume also that M is compact, Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
identifies this with
- H0(M,Z),
which can be identified with Z. Therefore cup product, under these hypotheses, does give rise to a symmetric bilinear form
Symmetric bilinear form
A symmetric bilinear form is a bilinear form on a vector space that is symmetric. Symmetric bilinear forms are of great importance in the study of orthogonal polarity and quadrics....
on H2k(M,Z); and therefore to a quadratic form Q. The form Q is non-degenerate due to Poincaré duality, as it pairs non-degenerately with itself. More generally, the signature can be defined in this way for any general compact polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
with 4n-dimensional Poincaré duality.
The signature of M is by definition the signature of Q. If M is not connected, its signature is defined to be the sum of the signatures of its connected components.
Other dimensions
If M has dimension not divisible by 4, its signature is usually defined to be 0. There are alternative generalization in L-theoryL-theory
Algebraic L-theory is the K-theory of quadratic forms; the term was coined by C. T. C. Wall,with L being used as the letter after K. Algebraic L-theory, also known as 'hermitian K-theory',is important in surgery theory.-Definition:...
: the signature can be interpreted as the 4k-dimensional (simply-connected) symmetric L-group
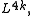or as the 4k-dimensional quadratic L-group 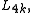and these invariants do not always vanish for other dimensions. The Kervaire invariant is a mod 2 (i.e., an element of 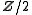) for framed manifolds of dimension 4k+2 (the quadratic L-group 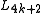), while the de Rham invariant is a mod 2 invariant of manifolds of dimension 4k+1 (the symmetric L-group 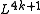); the other dimensional L-groups vanish.Kervaire invariant
When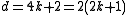 is twice an odd integer (singly even), the same construction gives rise to an antisymmetric bilinear form. Such forms do not have a signature invariant; if they are non-degenerate, any two such forms are equivalent. However, if one takes a quadratic refinement of the form, which occurs if one has a framed manifold, then the resulting ε-quadratic forms need not be equivalent, being distinguished by the Arf invariantArf invariant
In mathematics, the Arf invariant of a nonsingular quadratic form over a field of characteristic 2 was defined by when he started the systematic study of quadratic forms over arbitrary fields of characteristic2. The Arf invariant is the substitute, in...
. The resulting invariant of a manifold is called the Kervaire invariant.
Properties
René ThomRené Thom
René Frédéric Thom was a French mathematician. He made his reputation as a topologist, moving on to aspects of what would be called singularity theory; he became world-famous among the wider academic community and the educated general public for one aspect of this latter interest, his work as...
(1954) showed that the signature of a manifold is a cobordism invariant, and in particular is given by some linear combination of its Pontryagin
Lev Semenovich Pontryagin
Lev Semenovich Pontryagin was a Soviet mathematician. He was born in Moscow and lost his eyesight due to a primus stove explosion when he was 14...
numbers. Friedrich Hirzebruch
Friedrich Hirzebruch
Friedrich Ernst Peter Hirzebruch is a German mathematician, working in the fields of topology, complex manifolds and algebraic geometry, and a leading figure in his generation.-Life:He was born in Hamm, Westphalia...
(1954) found an explicit expression for this linear combination as the L genus of the manifold. William Browder
William Browder (mathematician)
William Browder is an American mathematician, specializing in algebraic topology, differential topology and differential geometry...
(1962) proved that a simply-connected compact polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
with 4n-dimensional Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
is homotopy equivalent to a manifold if and only if its signature satisfies the expression of the Hirzebruch signature theorem.
See also
- Hirzebruch signature theorem
- Genus of a multiplicative sequenceGenus of a multiplicative sequenceIn mathematics, the genus of a multiplicative sequence is a ring homomorphism, from the cobordism ring of smooth oriented compact manifolds to another ring, usually the ring of rational numbers.-Definition:...