
Signature operator
Encyclopedia
In mathematics
, the signature operator is an elliptic differential operator defined on a certain subspace of the space of differential form
s on an even-dimensional compact
Riemannian manifold
, whose analytic index is the same as the topological signature
of the manifold if the dimension of the manifold is a multiple of four. It is an instance of a Dirac-type operator.
 be a compact Riemannian manifold
be a compact Riemannian manifold
of even dimension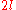 . Let
. Let
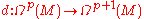
be the exterior derivative
on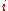 -th order differential forms on
-th order differential forms on  . The Riemannian metric on
. The Riemannian metric on  allows us to define the Hodge star operator
allows us to define the Hodge star operator  and with it the inner product
and with it the inner product
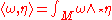
on forms. Denote by
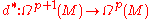
the adjoint operator
of the exterior differential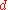 . This operator can be expressed purely in terms of the Hodge star operator as follows:
. This operator can be expressed purely in terms of the Hodge star operator as follows:
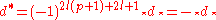
Now consider acting on the space of all forms
acting on the space of all forms 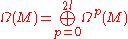 .
.
One way to consider this as a graded operator is the following: Let be an involution on the space of all forms defined by:
be an involution on the space of all forms defined by:
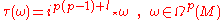
It is verified that anti-commutes with
anti-commutes with  and, consequently, switches the
and, consequently, switches the 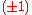 -eigenspaces
-eigenspaces 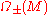 of
of 
Consequently,
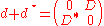
Definition: The operator with the above grading respectively the above operator
with the above grading respectively the above operator 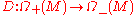 is called the signature operator of
is called the signature operator of  .
.
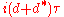 acting
acting
on the even-dimensional forms of .
.
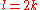 , so that the dimension of
, so that the dimension of  is a multiple of four, then Hodge theory
is a multiple of four, then Hodge theory
implies that:
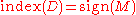
where the right hand side is the topological signature
(i.e. the signature of the quadratic form on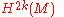 defined by the cup product
defined by the cup product
).
The Heat Equation approach to the Atiyah-Singer index theorem can then be used to show that:
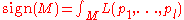
where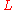 is the Hirzebruch L-Polynomial, and the
is the Hirzebruch L-Polynomial, and the 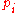 the Pontrjagin form
the Pontrjagin form
s on .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the signature operator is an elliptic differential operator defined on a certain subspace of the space of differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s on an even-dimensional compact
Closed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, whose analytic index is the same as the topological signature
Signature (topology)
In the mathematical field of topology, the signature is an integer invariant which is defined for an oriented manifold M of dimension d=4k divisible by four ....
of the manifold if the dimension of the manifold is a multiple of four. It is an instance of a Dirac-type operator.
Definition in the even-dimensional case
Let be a compact Riemannian manifold
be a compact Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
of even dimension
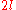 . Let
. Let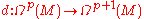
be the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
on
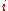 -th order differential forms on
-th order differential forms on  . The Riemannian metric on
. The Riemannian metric on  allows us to define the Hodge star operator
allows us to define the Hodge star operator  and with it the inner product
and with it the inner product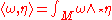
on forms. Denote by
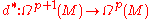
the adjoint operator
Hermitian adjoint
In mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator.Adjoints of operators generalize conjugate transposes of square matrices to infinite-dimensional situations...
of the exterior differential
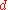 . This operator can be expressed purely in terms of the Hodge star operator as follows:
. This operator can be expressed purely in terms of the Hodge star operator as follows: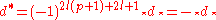
Now consider
 acting on the space of all forms
acting on the space of all forms 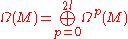 .
.One way to consider this as a graded operator is the following: Let
 be an involution on the space of all forms defined by:
be an involution on the space of all forms defined by: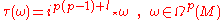
It is verified that
 anti-commutes with
anti-commutes with  and, consequently, switches the
and, consequently, switches the 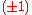 -eigenspaces
-eigenspaces 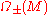 of
of 
Consequently,
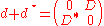
Definition: The operator
 with the above grading respectively the above operator
with the above grading respectively the above operator 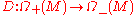 is called the signature operator of
is called the signature operator of  .
.Definition in the odd-dimensional case
In the odd dimensional case one defines the signature operator to be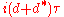 acting
actingon the even-dimensional forms of
 .
.Hirzebruch Signature Theorem
If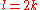 , so that the dimension of
, so that the dimension of  is a multiple of four, then Hodge theory
is a multiple of four, then Hodge theoryHodge theory
In mathematics, Hodge theory, named after W. V. D. Hodge, is one aspect of the study of the algebraic topology of a smooth manifold M. More specifically, it works out the consequences for the cohomology groups of M, with real coefficients, of the partial differential equation theory of generalised...
implies that:
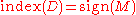
where the right hand side is the topological signature
Signature (topology)
In the mathematical field of topology, the signature is an integer invariant which is defined for an oriented manifold M of dimension d=4k divisible by four ....
(i.e. the signature of the quadratic form on
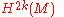 defined by the cup product
defined by the cup productCup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
).
The Heat Equation approach to the Atiyah-Singer index theorem can then be used to show that:
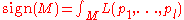
where
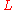 is the Hirzebruch L-Polynomial, and the
is the Hirzebruch L-Polynomial, and the 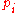 the Pontrjagin form
the Pontrjagin formPontryagin class
In mathematics, the Pontryagin classes are certain characteristic classes. The Pontryagin class lies in cohomology groups with degree a multiple of four...
s on
 .
.Homotopy invariance of the higher indices
Kaminker and Miller proved that the higher indices of the signature operator are homotopy-invariant.See also
- Hirzebruch signature theorem
- Pontryagin classPontryagin classIn mathematics, the Pontryagin classes are certain characteristic classes. The Pontryagin class lies in cohomology groups with degree a multiple of four...
- Friedrich HirzebruchFriedrich HirzebruchFriedrich Ernst Peter Hirzebruch is a German mathematician, working in the fields of topology, complex manifolds and algebraic geometry, and a leading figure in his generation.-Life:He was born in Hamm, Westphalia...
- Michael AtiyahMichael AtiyahSir Michael Francis Atiyah, OM, FRS, FRSE is a British mathematician working in geometry.Atiyah grew up in Sudan and Egypt but spent most of his academic life in the United Kingdom at Oxford and Cambridge, and in the United States at the Institute for Advanced Study...
- Isadore SingerIsadore SingerIsadore Manuel Singer is an Institute Professor in the Department of Mathematics at the Massachusetts Institute of Technology...

