Similitude is a concept applicable to the testing of engineering models

Model (physical)

A physical model is a smaller or larger physical copy of an object...

. A model is said to have similitude with the real application if the two share geometric similarity, kinematic similarity and dynamic similarity. Similarity

Similarity (geometry)

Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...

and similitude are interchangeable in this context.

The term dynamic similitude is often used as a catch-all because it implies that geometric and kinematic similitude have already been met.

Similitude's main application is in hydraulic and aerospace

Aerospace

Aerospace comprises the atmosphere of Earth and surrounding space. Typically the term is used to refer to the industry that researches, designs, manufactures, operates, and maintains vehicles moving through air and space...

 engineering to test fluid flow conditions with scaled

Scale (ratio)

The scale ratio of some sort of model which represents an original proportionally is the ratio of a linear dimension of the model to the same dimension of the original. Examples include a 3-dimensional scale model of a building or the scale drawings of the elevations or plans of a building. In such...

 models. It is also the primary theory behind many textbook formula

Formula

In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....

s in fluid mechanics

Fluid mechanics

Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...

.

Overview

Engineering models are used to study complex fluid dynamics problems where calculations and computer simulations aren't reliable. Models are usually smaller than the final design, but not always. Scale models allow testing of a design prior to building, and in many cases are a critical step in the development process.

Construction of a scale model, however, must be accompanied by an analysis to determine what conditions it is tested under. While the geometry may be simply scaled, other parameters, such as pressure

Pressure

Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...

, temperature

Temperature

Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...

 or the velocity

Velocity

In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...

 and type of fluid

Fluid

In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....

 may need to be altered. Similitude is achieved when testing conditions are created such that the test results are applicable to the real design.

The following criteria are required to achieve similitude;

• Geometric similarity
  Similarity (geometry)
  Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
  
  – The model is the same shape as the application, usually scaled.
• Kinematic similarity – Fluid flow of both the model and real application must undergo similar time rates of change motions. (fluid streamlines are similar)
• Dynamic similarity – Ratios of all forces acting on corresponding fluid particles and boundary surfaces in the two systems are constant.

To satisfy the above conditions the application is analyzed;

1. All parameters required to describe the system are identified using principles from continuum mechanics
   Continuum mechanics
   Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
   
   .
2. Dimensional analysis
   Dimensional analysis
   In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
   
    is used to express the system with as few independent variables and as many dimensionless parameters as possible.
3. The values of the dimensionless parameters are held to be the same for both the scale model and application. This can be done because they are dimensionless and will ensure dynamic similitude between the model and the application. The resulting equations are used to derive scaling laws which dictate model testing conditions.

It is often impossible to achieve strict similitude during a model test. The greater the departure from the application's operating conditions, the more difficult achieving similitude is. In these cases some aspects of similitude may be neglected, focusing on only the most important parameters.

The design of marine vessels remains more of an art than a science in
large part because dynamic similitude is especially difficult to attain
for a vessel that is partially submerged: a ship is affected by wind
forces in the air above it, by hydrodynamic forces within the water
under it, and especially by wave motions at the interface between the
water and the air. The scaling requirements for each of these
phenomena differ, so models cannot replicate what happens to a full
sized vessel nearly so well as can be done for an aircraft or
submarine—each of which operates entirely within one medium.

Similitude is a term used widely in fracture mechanics relating to the strain life approach. Under given loading conditions the fatigue damage in an un-notched specimen is comparable to that of a notched specimen. Similitude suggests that the component fatigue life of the two objects will also be similar.

An example

Consider a submarine

Submarine

A submarine is a watercraft capable of independent operation below the surface of the water. It differs from a submersible, which has more limited underwater capability...

 modeled at 1/40th scale. The application operates in sea water at 0.5 °C, moving at 5 m/s. The model will be tested in fresh water at 20 °C. Find the power required for the submarine to operate at the stated speed.

A free body diagram

Free body diagram

A free body diagram, also called a force diagram, is a pictorial representation often used by physicists and engineers to analyze the forces acting on a body of interest. A free body diagram shows all forces of all types acting on this body. Drawing such a diagram can aid in solving for the unknown...

 is constructed and the relevant relationships of force and velocity are formulated using techniques from continuum mechanics

Continuum mechanics

Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...

. The variables which describe the system are:

Variable	Application	Scaled mode	Units
L (diameter Length In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...  of submarine)	1	1/40	(m)
V (speed Speed In kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as... )	5	calculate	(m/s)
(density Density The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight... )	1028	998	(kg/m3)
(dynamic viscosity Viscosity Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity... )	1.88x10−3	1.00x10−3	Pa Pascal (unit) The pascal is the SI derived unit of pressure, internal pressure, stress, Young's modulus and tensile strength, named after the French mathematician, physicist, inventor, writer, and philosopher Blaise Pascal. It is a measure of force per unit area, defined as one newton per square metre... ·s (N s/m2)
F (force Force In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform... )	calculate	to be measured	N   (kg m/s2)

This example has five independent variables and three fundamental units. The fundamental units are: metre

Metre

The metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology...

, kilogram

Kilogram

The kilogram or kilogramme , also known as the kilo, is the base unit of mass in the International System of Units and is defined as being equal to the mass of the International Prototype Kilogram , which is almost exactly equal to the mass of one liter of water...

, second

Second

The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....

.

Invoking the Buckingham π theorem shows that the system can be described with two dimensionless numbers and one independent variable.

Dimensional analysis is used to re-arrange the units to form the Reynolds number (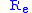) and pressure coefficient

Pressure coefficient

The pressure coefficient is a dimensionless number which describes the relative pressures throughout a flow field in fluid dynamics. The pressure coefficient is used in aerodynamics and hydrodynamics...

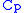 (). These dimensionless numbers account for all the variables listed above except F, which will be the test measurement. Since the dimensionless parameters will stay constant for both the test and the real application, they will be used to formulate scaling laws for the test.

Scaling laws:

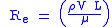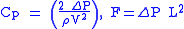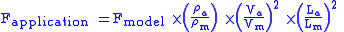This gives a required test velocity of:

.

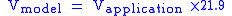The force measured from the model at that velocity is then scaled to find the force that can be expected for the real application:



The power in watts required by the submarine is then:



Note that even though the model is scaled smaller, the water velocity needs to be increased for testing. This remarkable result shows how similitude in nature is often counterintuitive.

Typical applications

Similitude has been well documented for a large number of engineering problems and is the basis of many textbook formulas and dimensionless quantities. These formulas and quantities are easy to use without having to repeat the laborious task of dimensional analysis and formula derivation. Simplification of the formulas (by neglecting some aspects of similitude) is common, and needs to be reviewed by the engineer for each application.

Similitude can be used to predict the performance of a new design based on data from an existing, similar design. In this case, the model is the existing design. Another use of similitude and models is in validation of computer simulation

Computer simulation

A computer simulation, a computer model, or a computational model is a computer program, or network of computers, that attempts to simulate an abstract model of a particular system...

s with the ultimate goal of eliminating the need for physical models altogether.

Another application of similitude is to replace the operating fluid with a different test fluid. Wind tunnels, for example, have trouble with air liquefying in certain conditions so helium

Helium

Helium is the chemical element with atomic number 2 and an atomic weight of 4.002602, which is represented by the symbol He. It is a colorless, odorless, tasteless, non-toxic, inert, monatomic gas that heads the noble gas group in the periodic table...

 is sometimes used. Other applications may operate in dangerous or expensive fluids so the testing is carried out in a more convenient substitute.

Some common applications of similitude and associated dimensionless numbers;

Incompressible flow (see example above)–	Reynolds number, Pressure coefficient Pressure coefficient The pressure coefficient is a dimensionless number which describes the relative pressures throughout a flow field in fluid dynamics. The pressure coefficient is used in aerodynamics and hydrodynamics... , (Froude number Froude number The Froude number is a dimensionless number defined as the ratio of a characteristic velocity to a gravitational wave velocity. It may equivalently be defined as the ratio of a body's inertia to gravitational forces. In fluid mechanics, the Froude number is used to determine the resistance of an...  and Weber number Weber number The Weber number is a dimensionless number in fluid mechanics that is often useful in analysing fluid flows where there is an interface between two different fluids, especially for multiphase flows with strongly curved surfaces. It can be thought of as a measure of the relative importance of the...  for open channel hydraulics)
Compressible flows –	Reynolds number, Mach number Mach number Mach number is the speed of an object moving through air, or any other fluid substance, divided by the speed of sound as it is in that substance for its particular physical conditions, including those of temperature and pressure... , Prandtl number, Specific heat ratio
Flow-excited vibration	Strouhal number Strouhal number In dimensional analysis, the Strouhal number is a dimensionless number describing oscillating flow mechanisms. The parameter is named after Vincenc Strouhal, a Czech physicist who experimented in 1878 with wires experiencing vortex shedding and singing in the wind...
Centrifugal compressors –	Reynolds number, Mach number Mach number Mach number is the speed of an object moving through air, or any other fluid substance, divided by the speed of sound as it is in that substance for its particular physical conditions, including those of temperature and pressure... , Pressure coefficient Pressure coefficient The pressure coefficient is a dimensionless number which describes the relative pressures throughout a flow field in fluid dynamics. The pressure coefficient is used in aerodynamics and hydrodynamics... , Velocity ratio Velocity ratio Velocity Ratio is defined by Classical mechanics as the distance that the point of Effort moved divided by the distance that the point of Load moved as given from here Thus VR = Distance / Distance =...
Boundary layer thickness –	Reynolds number, Womersley number Womersley number The Womersley number is a dimensionless number in biofluid mechanics. It is a dimensionless expression of the pulsatile flow frequency in relation to viscous effects. It is named after John R. Womersley . The Womersley number is important in keeping dynamic similarity when scaling an experiment. An... , Dynamic similarity

See also

• Dimensionless number
• Buckingham π theorem
• Dimensional analysis
  Dimensional analysis
  In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
  
  
• MKS system of fundamental units
  Si
  Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
  
  
• Dynamic similarity (Reynolds and Womersley numbers)

External links

• MIT open courseware lecture notes on Similitude for marine engineering (pdf file)