Simple set
Encyclopedia
In recursion theory
a subset of the natural numbers is called a simple set if it is recursively enumerable, but every infinite subset of its complement fails to be enumerated recursively. Simple sets are examples of recursively enumerable sets, that are not recursive (--- a set is recursive if and only if both the set and its complement are recursively enumerable).
in the search for a non-Turing-complete recursively enumerable set. Whether such sets exist is known as Post's problem. Post had to prove two things in order to obtain his result, one is that the simple set, say A, does not Turing-reduce to the empty set, and that the K, the halting problem
, does not Turing-reduce to A. He succeeded in the first part (which is obvious by definition), but for the other part, he managed only to prove a many-one reduction
.
It was affirmed by Friedberg and Muchnik in the 1950s using a novel technique called the priority method. They give a construction for a set that is simple (and thus non-recursive), but fails to compute the halting problem.
we have that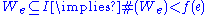
.
Recursion theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
a subset of the natural numbers is called a simple set if it is recursively enumerable, but every infinite subset of its complement fails to be enumerated recursively. Simple sets are examples of recursively enumerable sets, that are not recursive (--- a set is recursive if and only if both the set and its complement are recursively enumerable).
Relation to Post's problem
Simple sets were devised by Emil Leon PostEmil Leon Post
Emil Leon Post was a mathematician and logician. He is best known for his work in the field that eventually became known as computability theory.-Early work:...
in the search for a non-Turing-complete recursively enumerable set. Whether such sets exist is known as Post's problem. Post had to prove two things in order to obtain his result, one is that the simple set, say A, does not Turing-reduce to the empty set, and that the K, the halting problem
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
, does not Turing-reduce to A. He succeeded in the first part (which is obvious by definition), but for the other part, he managed only to prove a many-one reduction
Many-one reduction
In computability theory and computational complexity theory, a many-one reduction is a reduction which converts instances of one decision problem into instances of a second decision problem. Reductions are thus used to measure the relative computational difficulty of two problems.Many-one...
.
It was affirmed by Friedberg and Muchnik in the 1950s using a novel technique called the priority method. They give a construction for a set that is simple (and thus non-recursive), but fails to compute the halting problem.
Formal definitions and some properties
- A set
is called immune iff 
is infinite, but for every index 
, we have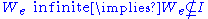 
. Or equivalently: there is no infinite subset of 
that is recursively enumerable. - A set
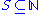is called simple iff it is recursively enumerable and its complement is immune. - A set
is called effectively immune iff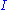 
is infinite, but there exists a recursive function 
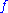such that for every index 
,
we have that
.
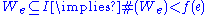- A set
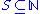is called effectively simple if it is recursively enumerable and its complement is effectively immune. Every effectively simple set, is simple and Turing-complete.