Single precision floating-point format
Encyclopedia
Single-precision floating-point format is a computer number format that occupies 4 bytes (32 bits) in computer memory and represents a wide dynamic range of values by using a floating point
.
In IEEE 754-2008 the 32-bit base 2 format is officially referred to as binary32. It was called single in IEEE 754-1985.
In older computers, other floating-point formats of 4 bytes were used.
One of the first programming language
s to provide single- and double-precision floating-point data types was Fortran
.
Before the widespread adoption of IEEE 754-1985, the representation and properties of the double float data type depended on the computer manufacturer and computer model.
Single-precision binary floating-point is used due to its wider range over fixed point
(of the same bit-width), even if at the cost of precision.
Single precision is known as float in C
, C++, C#, Java
, and Haskell
, and as single in Pascal
, Visual Basic, and MATLAB
. However, float in Python
and single in versions of Octave
prior to 3.2 refer to double-precision numbers.
Sign bit determines the sign of the number, which is the sign of the significand as well. Exponent is either an 8 bit signed integer from −127 to 128 or an 8 bit unsigned integer from 0 to 255 which is the accepted biased form in IEEE 754 binary32 definition. For this case an exponent value of 127 represents the actual zero.
The true significand includes 23 fraction bits to the right of the binary point and an implicit leading bit (to the left of the binary point) with value 1 unless the exponent is stored with all zeros. Thus only 23 fraction bits of the significand
appear in the memory format but the total precision is 24 bits (equivalent to log10(224) ≈ 7.225 decimal digits). The bits are laid out as follows:
The real value assumed by a given 32 bit binary32 data with a given biased exponent e
and a 23 bit fraction is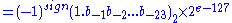
where more precisely we have :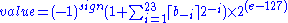
Thus, in order to get the true exponent as defined by the offset binary representation, the offset of 127 has to be subtracted from the stored exponent.
The stored exponents 00H and FFH are interpreted specially.
The minimum positive (subnormal) value is
2−149 ≈ 1.4 × 10−45.
The minimum positive normal value is 2−126 ≈ 1.18 × 10−38.
The maximum representable value is (2−2−23) × 2127 ≈ 3.4 × 1038.
of a real number into its equivalent binary32 format.
Here we can show how to convert a base 10 real number into an IEEE 754 binary32 format
using the following outline :
Conversion of the fractional part:
consider 0.375, the fractional part of 12.375. To convert it into a binary fraction, multiply the fraction by 2, take the integer part and re-multiply new fraction by 2 until a fraction of zero is found or until the precision limit is reached which is 23 fraction digits for IEEE 754 binary32 format.
0.375 x 2 = 0.750 = 0 + 0.750 => b−1 = 0, the integer part represents the binary fraction digit. Re-multiply 0.750 by 2 to proceed
0.750 x 2 = 1.500 = 1 + 0.500 => b−2 = 1
0.500 x 2 = 1.000 = 1 + 0.000 => b−3 = 1, fraction = 0.000, terminate
We see that (0.375)10 can be exactly represented in binary as (0.011)2. Not all decimal fractions can be represented in a finite digit binary fraction. For example decimal 0.1 cannot be represented in binary exactly. So it is only approximated.
Therefore (12.375)10 = (12)10 + (0.375)10 = (1100)2 + (0.011)2 = (1100.011)2
Also IEEE 754 binary32 format requires that you represent real values in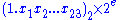
format, (see Normalized number
, Denormalized number) so that 1100.011 is shifted to the left by 3 digits to become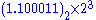
Finally we can see that: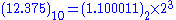
From which we deduce:
From these we can form the resulting 32 bit IEEE 754 binary32 format representation of
12.375 as: 0-10000010-10001100000000000000000 = 41460000H
Note: consider converting 68.123 into IEEE 754 binary32 format:
Using the above procedure you expect to get 42883EF9H with the last 4 bits being 1001
However due to the default rounding behaviour of IEEE 754 format what you get is 42883EFAH whose last 4 bits are 1010 .
Ex 1:
Consider decimal 1
We can see that :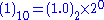
From which we deduce :
From these we can form the resulting 32 bit IEEE 754 binary32 format representation of
real number 1 as: 0-01111111-00000000000000000000000 = 3f800000H
Ex 2:
Consider a value 0.25 .
We can see that :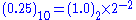
From which we deduce :
From these we can form the resulting 32 bit IEEE 754 binary32 format representation of
real number 0.25 as: 0-01111101-00000000000000000000000 = 3e800000H
Ex 3:
Consider a value of 0.375 . We saw that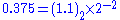
Hence after determining a representation of 0.375 as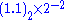
we can proceed as above :
From these we can form the resulting 32 bit IEEE 754 binary32 format representation of
real number 0.375 as: 0-01111101-10000000000000000000000 = 3ec00000H
,
of the floating-point value. This includes the sign, (biased) exponent, and significand.
3f80 0000 = 1
c000 0000 = −2
7f7f ffff ≈ 3.4028234 × 1038 (max single precision)
0000 0000 = 0
8000 0000 = −0
7f80 0000 = infinity
ff80 0000 = −infinity
3eaa aaab ≈ 1/3
By default, 1/3 rounds up instead of down like double precision
, because of the even number of bits in the significand.
So the bits beyond the rounding point are
.
41c8 000016 = 0100 0001 1100 1000 0000 0000 0000 00002
then we break it down into three parts; sign bit, exponent and significand.
Sign bit: 0
Exponent: 1000 00112 = 8316 = 131
Significand: 100 1000 0000 0000 0000 00002 = 48000016
We then add the implicit 24th bit to the significand
Significand: 1100 1000 0000 0000 0000 00002 = C8000016
and decode the exponent value by subtracting 127
Raw exponent: 8316 = 131
Decoded exponent: 131 − 127 = 4
Each of the 24 bits of the significand, bit 23 to bit 0, represents a value, starting at 1 and halves for each bit, as follows
bit 23 = 1
bit 22 = 0.5
bit 21 = 0.25
bit 20 = 0.125
bit 19 = 0.0625
.
.
bit 0 = 0.00000011920928955078125
The significand in this example has three bits set, bit 23, bit 22 and bit 19. We can now decode the significand
by adding the values represented by these bits.
Decoded significand: 1 + 0.5 + 0.0625 = 1.5625 = C80000/223
Then we need to multiply with the base, 2, to the power of the exponent to get the final result
1.5625 × 24 = 25
Thus
41c8 0000 = 25
This is equivalent to:
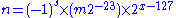
where
is the sign bit, 
is the exponent, and 
is the significand in base 10.
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
.
In IEEE 754-2008 the 32-bit base 2 format is officially referred to as binary32. It was called single in IEEE 754-1985.
In older computers, other floating-point formats of 4 bytes were used.
One of the first programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s to provide single- and double-precision floating-point data types was Fortran
Fortran
Fortran is a general-purpose, procedural, imperative programming language that is especially suited to numeric computation and scientific computing...
.
Before the widespread adoption of IEEE 754-1985, the representation and properties of the double float data type depended on the computer manufacturer and computer model.
Single-precision binary floating-point is used due to its wider range over fixed point
Fixed-point arithmetic
In computing, a fixed-point number representation is a real data type for a number that has a fixed number of digits after the radix point...
(of the same bit-width), even if at the cost of precision.
Single precision is known as float in C
C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
, C++, C#, Java
Java (programming language)
Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
, and Haskell
Haskell (programming language)
Haskell is a standardized, general-purpose purely functional programming language, with non-strict semantics and strong static typing. It is named after logician Haskell Curry. In Haskell, "a function is a first-class citizen" of the programming language. As a functional programming language, the...
, and as single in Pascal
Pascal (programming language)
Pascal is an influential imperative and procedural programming language, designed in 1968/9 and published in 1970 by Niklaus Wirth as a small and efficient language intended to encourage good programming practices using structured programming and data structuring.A derivative known as Object Pascal...
, Visual Basic, and MATLAB
MATLAB
MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
. However, float in Python
Python (programming language)
Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
and single in versions of Octave
GNU Octave
GNU Octave is a high-level language, primarily intended for numerical computations. It provides a convenient command-line interface for solving linear and nonlinear problems numerically, and for performing other numerical experiments using a language that is mostly compatible with MATLAB...
prior to 3.2 refer to double-precision numbers.
IEEE 754 single-precision binary floating-point format: binary32
The IEEE 754 standard specifies a binary32 as having:- Sign bitSign bitIn computer science, the sign bit is a bit in a computer numbering format that indicates the sign of a number. In IEEE format, the sign bit is the leftmost bit...
: 1 bit - Exponent width: 8 bits
- SignificandSignificandThe significand is part of a floating-point number, consisting of its significant digits. Depending on the interpretation of the exponent, the significand may represent an integer or a fraction.-Examples:...
precisionPrecision (arithmetic)The precision of a value describes the number of digits that are used to express that value. In a scientific setting this would be the total number of digits or, less commonly, the number of fractional digits or decimal places...
: 24 (23 explicitly stored)
Sign bit determines the sign of the number, which is the sign of the significand as well. Exponent is either an 8 bit signed integer from −127 to 128 or an 8 bit unsigned integer from 0 to 255 which is the accepted biased form in IEEE 754 binary32 definition. For this case an exponent value of 127 represents the actual zero.
The true significand includes 23 fraction bits to the right of the binary point and an implicit leading bit (to the left of the binary point) with value 1 unless the exponent is stored with all zeros. Thus only 23 fraction bits of the significand
Significand
The significand is part of a floating-point number, consisting of its significant digits. Depending on the interpretation of the exponent, the significand may represent an integer or a fraction.-Examples:...
appear in the memory format but the total precision is 24 bits (equivalent to log10(224) ≈ 7.225 decimal digits). The bits are laid out as follows:
The real value assumed by a given 32 bit binary32 data with a given biased exponent e
and a 23 bit fraction is
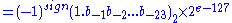
where more precisely we have :
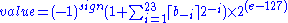
Exponent encoding
The single-precision binary floating-point exponent is encoded using an offset-binary representation, with the zero offset being 127; also known as exponent bias in the IEEE 754 standard.- Emin = 01H−7FH = −126
- Emax = FEH−7FH = 127
- Exponent biasExponent biasIn IEEE 754 floating point numbers, the exponent is biased in the engineering sense of the word – the value stored is offset from the actual value by the exponent bias....
= 7FH = 127
Thus, in order to get the true exponent as defined by the offset binary representation, the offset of 127 has to be subtracted from the stored exponent.
The stored exponents 00H and FFH are interpreted specially.
| Exponent | Significand zero | Significand non-zero | Equation |
|---|---|---|---|
| 00H | zero 0 (number) 0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems... , −0 |
subnormal numbers | (−1)signbits×2−126× 0.significandbits |
| 01H, ..., FEH | normalized value | (−1)signbits×2exponentbits−127× 1.significandbits | |
| FFH | ±infinity Infinity Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity... |
NaN NaN In computing, NaN is a value of the numeric data type representing an undefined or unrepresentable value, especially in floating-point calculations... (quiet, signalling) |
|
The minimum positive (subnormal) value is
2−149 ≈ 1.4 × 10−45.
The minimum positive normal value is 2−126 ≈ 1.18 × 10−38.
The maximum representable value is (2−2−23) × 2127 ≈ 3.4 × 1038.
Converting from decimal representation to binary32 format
In general refer to the IEEE 754 standard itself for the strict conversion (including the rounding behaviour)of a real number into its equivalent binary32 format.
Here we can show how to convert a base 10 real number into an IEEE 754 binary32 format
using the following outline :
- consider a real number with an integer and a fraction part such as 12.375
- convert and normalizeNormalized numberA real number is called normalized, if it is in the form:\pm d_0.d_1d_2d_3\dots\times 10^nwhere n is an integer, d_0, d_1, d_2, d_3... are the digits of the number in base 10, and d_0 is not zero....
the integer part into binaryBinary numeral systemThe binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2... - convert the fraction part using the following technique as shown here
- add the two results and adjust them to produce a proper final conversion
Conversion of the fractional part:
consider 0.375, the fractional part of 12.375. To convert it into a binary fraction, multiply the fraction by 2, take the integer part and re-multiply new fraction by 2 until a fraction of zero is found or until the precision limit is reached which is 23 fraction digits for IEEE 754 binary32 format.
0.375 x 2 = 0.750 = 0 + 0.750 => b−1 = 0, the integer part represents the binary fraction digit. Re-multiply 0.750 by 2 to proceed
0.750 x 2 = 1.500 = 1 + 0.500 => b−2 = 1
0.500 x 2 = 1.000 = 1 + 0.000 => b−3 = 1, fraction = 0.000, terminate
We see that (0.375)10 can be exactly represented in binary as (0.011)2. Not all decimal fractions can be represented in a finite digit binary fraction. For example decimal 0.1 cannot be represented in binary exactly. So it is only approximated.
Therefore (12.375)10 = (12)10 + (0.375)10 = (1100)2 + (0.011)2 = (1100.011)2
Also IEEE 754 binary32 format requires that you represent real values in
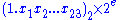format, (see Normalized numberNormalized number
A real number is called normalized, if it is in the form:\pm d_0.d_1d_2d_3\dots\times 10^nwhere n is an integer, d_0, d_1, d_2, d_3... are the digits of the number in base 10, and d_0 is not zero....
, Denormalized number) so that 1100.011 is shifted to the left by 3 digits to become
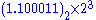
Finally we can see that:
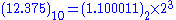
From which we deduce:
- The exponent is 3 (and in the biased form it is therefore 130 = 1000 0010)
- The fraction is 100011 (looking to the right of the binary point)
From these we can form the resulting 32 bit IEEE 754 binary32 format representation of
12.375 as: 0-10000010-10001100000000000000000 = 41460000H
Note: consider converting 68.123 into IEEE 754 binary32 format:
Using the above procedure you expect to get 42883EF9H with the last 4 bits being 1001
However due to the default rounding behaviour of IEEE 754 format what you get is 42883EFAH whose last 4 bits are 1010 .
Ex 1:
Consider decimal 1
We can see that :
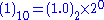
From which we deduce :
- The exponent is 0 (and in the biased form it is therefore 127 = 0111 1111 )
- The fraction is 0 (looking to the right of the binary point in 1.0 is all 0 = 000...0)
From these we can form the resulting 32 bit IEEE 754 binary32 format representation of
real number 1 as: 0-01111111-00000000000000000000000 = 3f800000H
Ex 2:
Consider a value 0.25 .
We can see that :
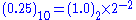
From which we deduce :
- The exponent is −2 (and in the biased form it is 127+(−2)= 125 = 0111 1101 )
- The fraction is 0 (looking to the right of binary point in 1.0 is all zeros)
From these we can form the resulting 32 bit IEEE 754 binary32 format representation of
real number 0.25 as: 0-01111101-00000000000000000000000 = 3e800000H
Ex 3:
Consider a value of 0.375 . We saw that
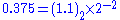
Hence after determining a representation of 0.375 as
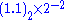
we can proceed as above :
- The exponent is −2 (and in the biased form it is 127+(−2)= 125 = 0111 1101 )
- The fraction is 1 (looking to the right of binary point in 1.1 is a single 1 = x1)
From these we can form the resulting 32 bit IEEE 754 binary32 format representation of
real number 0.375 as: 0-01111101-10000000000000000000000 = 3ec00000H
Single-precision examples
These examples are given in bit representation, in hexadecimalHexadecimal
In mathematics and computer science, hexadecimal is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F to represent values ten to fifteen...
,
of the floating-point value. This includes the sign, (biased) exponent, and significand.
3f80 0000 = 1
c000 0000 = −2
7f7f ffff ≈ 3.4028234 × 1038 (max single precision)
0000 0000 = 0
8000 0000 = −0
7f80 0000 = infinity
ff80 0000 = −infinity
3eaa aaab ≈ 1/3
By default, 1/3 rounds up instead of down like double precision
Double precision
In computing, double precision is a computer number format that occupies two adjacent storage locations in computer memory. A double-precision number, sometimes simply called a double, may be defined to be an integer, fixed point, or floating point .Modern computers with 32-bit storage locations...
, because of the even number of bits in the significand.
So the bits beyond the rounding point are
1010... which is more than 1/2 of a unit in the last placeUnit in the Last Place
In computer science and numerical analysis, unit in the last place or unit of least precision is the spacing between floating-point numbers, i.e., the value the least significant bit represents if it is 1...
.
Converting from single-precision binary to decimal
We start with the hexadecimal representation of the value, 41c80000, in this example, and convert it to binary41c8 000016 = 0100 0001 1100 1000 0000 0000 0000 00002
then we break it down into three parts; sign bit, exponent and significand.
Sign bit: 0
Exponent: 1000 00112 = 8316 = 131
Significand: 100 1000 0000 0000 0000 00002 = 48000016
We then add the implicit 24th bit to the significand
Significand: 1100 1000 0000 0000 0000 00002 = C8000016
and decode the exponent value by subtracting 127
Raw exponent: 8316 = 131
Decoded exponent: 131 − 127 = 4
Each of the 24 bits of the significand, bit 23 to bit 0, represents a value, starting at 1 and halves for each bit, as follows
bit 23 = 1
bit 22 = 0.5
bit 21 = 0.25
bit 20 = 0.125
bit 19 = 0.0625
.
.
bit 0 = 0.00000011920928955078125
The significand in this example has three bits set, bit 23, bit 22 and bit 19. We can now decode the significand
by adding the values represented by these bits.
Decoded significand: 1 + 0.5 + 0.0625 = 1.5625 = C80000/223
Then we need to multiply with the base, 2, to the power of the exponent to get the final result
1.5625 × 24 = 25
Thus
41c8 0000 = 25
This is equivalent to:
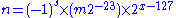
where
is the sign bit, is the exponent, and is the significand in base 10.See also
- IEEE Standard for Floating-Point Arithmetic (IEEE 754)
- ISO/IEC 10967ISO/IEC 10967ISO/IEC 10967, Language independent arithmetic , is a series ofstandards on computer arithmetic. It is compatible with IEC 60559, and indeed much of thespecifications in parts 2 and 3 are for IEEE 754 special values...
, Language Independent Arithmetic - Primitive data type
- Numerical stabilityNumerical stabilityIn the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
- Double-precision floating-point format