Singular point of an algebraic variety
Encyclopedia
In mathematics
, a singular point of an algebraic variety
V is a point P that is 'special' (so, singular), in the geometric sense that V is not locally flat
there. In the case of an algebraic curve
, a plane curve
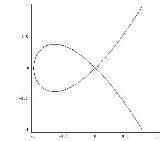
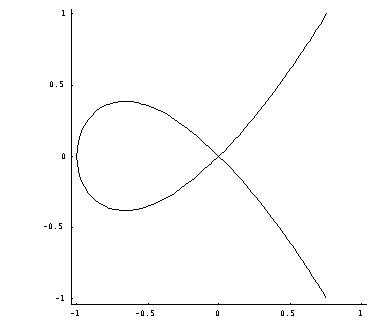
that has a double point, such as the cubic curve
exhibits at (0, 0), cannot simply be parametrized near the origin. A plot of this curve is below with the singular point at the origin. An example of singular point is when a graph crosses over itself:
The reason for that algebraically is that both sides of the equation show powers higher than 1 of the variables x and y. In terms of differential calculus
, if
so that the curve has equation
then the partial derivative
s of F with respect to both x and y vanish at (0,0). This means that if we try to use the implicit function theorem
to express y as a function of x near y = 0, we shall fail; and indeed no linear combination of x and y is a function of another essentially different one, so that this is a geometric condition not tied to any choice of coordinate axes.
In general for a hypersurface
the singular points are those at which all the partial derivatives simultaneously vanish. A general algebraic variety V being defined by several polynomials, or in algebraic terms an ideal
of polynomials, the condition on a point P to be a singular point of V is that the linear parts of those polynomials are linearly dependent, when written in terms of variables Xi − Pi
that make P the origin of coordinates.
Points of V that are not singular are called non-singular or regular. It is always true that most points are non-singular in the sense that the non-singular points form a set that is both open and non-empty.
It is important to note that the geometric criterion for a point of a variety to be singular (mentioned earlier), that it is a point where the variety is not "locally flat", can be very hard to recognize for varieties over a general field. The work of Milnor and others shows that, over the complex numbers, the statement is precisely true in every reasonable interpretation. But, as Milnor points out, over the real numbers "The equation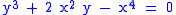
... can actually be solved for 
as a real analytic function of 
" (so that the variety it defines is the graph of a real analytic function, and therefore a real analytic manifold) "but this equation also defines a variety having a singular point at the origin". Obviously the "geometric" meaning of "locally flat" over fields of finite characteristic, or ultrametric fields, is even more vexed.
mappings, (functions from M to Rn where all derivatives exist). Analysis of these singular points can be reduced to the algebraic variety case by considering the jets
of the mapping. The k-th jet is the Taylor series
of the mapping truncated at degree k and deleting the constant term
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a singular point of an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
V is a point P that is 'special' (so, singular), in the geometric sense that V is not locally flat
Local flatness
In topology, a branch of mathematics, local flatness is a property of a submanifold in a topological manifold of larger dimension.Suppose a d dimensional manifold N is embedded in an n dimensional manifold M...
there. In the case of an algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
, a plane curve
Plane curve
In mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....
that has a double point, such as the cubic curve
- y2 = x2(x + 1)
exhibits at (0, 0), cannot simply be parametrized near the origin. A plot of this curve is below with the singular point at the origin. An example of singular point is when a graph crosses over itself:
The reason for that algebraically is that both sides of the equation show powers higher than 1 of the variables x and y. In terms of differential calculus
Differential calculus
In mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
, if
- F(x,y) = y2 − x2(x + 1),
so that the curve has equation
- F(x,y) = 0,
then the partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of F with respect to both x and y vanish at (0,0). This means that if we try to use the implicit function theorem
Implicit function theorem
In multivariable calculus, the implicit function theorem is a tool which allows relations to be converted to functions. It does this by representing the relation as the graph of a function. There may not be a single function whose graph is the entire relation, but there may be such a function on...
to express y as a function of x near y = 0, we shall fail; and indeed no linear combination of x and y is a function of another essentially different one, so that this is a geometric condition not tied to any choice of coordinate axes.
In general for a hypersurface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
- F(x, y, z, ...) = 0
the singular points are those at which all the partial derivatives simultaneously vanish. A general algebraic variety V being defined by several polynomials, or in algebraic terms an ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of polynomials, the condition on a point P to be a singular point of V is that the linear parts of those polynomials are linearly dependent, when written in terms of variables Xi − Pi
that make P the origin of coordinates.
Points of V that are not singular are called non-singular or regular. It is always true that most points are non-singular in the sense that the non-singular points form a set that is both open and non-empty.
It is important to note that the geometric criterion for a point of a variety to be singular (mentioned earlier), that it is a point where the variety is not "locally flat", can be very hard to recognize for varieties over a general field. The work of Milnor and others shows that, over the complex numbers, the statement is precisely true in every reasonable interpretation. But, as Milnor points out, over the real numbers "The equation
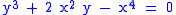... can actually be solved for as a real analytic function of " (so that the variety it defines is the graph of a real analytic function, and therefore a real analytic manifold) "but this equation also defines a variety having a singular point at the origin". Obviously the "geometric" meaning of "locally flat" over fields of finite characteristic, or ultrametric fields, is even more vexed.Singular points of smooth mappings
As the notion of singular points is a purely local property the above definition can be extended to cover the wider class of smoothSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
mappings, (functions from M to Rn where all derivatives exist). Analysis of these singular points can be reduced to the algebraic variety case by considering the jets
Jet (mathematics)
In mathematics, the jet is an operation which takes a differentiable function f and produces a polynomial, the truncated Taylor polynomial of f, at each point of its domain...
of the mapping. The k-th jet is the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
of the mapping truncated at degree k and deleting the constant term
Constant term
In mathematics, a constant term is a term in an algebraic expression has a value that is constant or cannot change, because it does not contain any modifiable variables. For example, in the quadratic polynomialx^2 + 2x + 3,\ the 3 is a constant term....
.