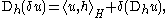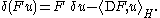Skorokhod integral
Encyclopedia
In mathematics
, the Skorokhod integral, often denoted δ, is an operator of great importance in the theory of stochastic processes. It is named after the Ukrainian
mathematician
Anatoliy Skorokhod
. Part of its importance is that it unifies several concepts:
(Ω, Σ, P) and a Hilbert space
H; E denotes expectation
with respect to P:
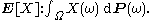
Intuitively speaking, the Malliavin derivative of a random variable F in Lp(Ω) is defined by expanding it in terms of Gaussian random variables that are parametrized by the elements of H and differentiating the expansion formally; the Skorokhod integral is the adjoint operation to the Malliavin derivative.
Consider a family of R-valued random variables W(h), indexed by the elements h of the Hilbert space H. Assume further that each W(h) is a Gaussian (normal) random variable, that the map taking h to W(h) is a linear map, and that the mean
and covariance
structure is given by
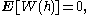
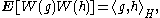
for all g and h in H. It can be shown that, given H, there always exists a probability space (Ω, Σ, P) and a family of random variables with the above properties. The Malliavin derivative is essentially defined by formally setting the derivative of the random variable W(h) to be h, and then extending this definition to “smooth enough
” random variables. For a random variable F of the form
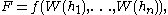
where f : Rn → R is smooth, the Malliavin derivative is defined using the earlier “formal definition” and the chain rule:
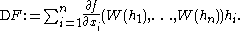
In other words, whereas F was a real-valued random variable, its derivative DF is an H-valued random variable, an element of the space Lp(Ω;H). Of course, this procedure only defines DF for “smooth” random variables, but an approximation procedure can be employed to define DF for F in a large subspace of Lp(Ω); the domain
of D is the closure
of the smooth random variables in the seminorm
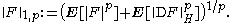
This space is denoted by D1,p and is called the Watanabe-Sobolev space.
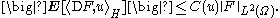
The Skorokhod integral of a process u in L2(Ω; H) is a real-valued random variable δu in L2(Ω); if u lies in the domain of δ, then δu is defined by the relation that, for all F ∈ D1,2,

Just as the Malliavin derivative D was first defined on simple, smooth random variables, the Skorokhod integral has a simple expression for “simple processes”: if u is given by

with Fj smooth and hj in H, then
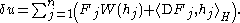
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Skorokhod integral, often denoted δ, is an operator of great importance in the theory of stochastic processes. It is named after the Ukrainian
Ukraine
Ukraine is a country in Eastern Europe. It has an area of 603,628 km², making it the second largest contiguous country on the European continent, after Russia...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Anatoliy Skorokhod
Anatoliy Skorokhod
Anatoliy Volodymyrovych Skorokhod was a Soviet and Ukrainian mathematician, and an academician of the National Academy of Sciences of Ukraine from 1985 to his death in 2011....
. Part of its importance is that it unifies several concepts:
- δ is an extension of the Itō integral to non-adapted processAdapted processIn the study of stochastic processes, an adapted process is one that cannot "see into the future". An informal interpretation is that X is adapted if and only if, for every realisation and every n, Xn is known at time n...
es; - δ is the adjoint of the Malliavin derivativeMalliavin derivativeIn mathematics, the Malliavin derivative is a notion of derivative in the Malliavin calculus. Intuitively, it is the notion of derivative appropriate to paths in classical Wiener space, which are "usually" not differentiable in the usual sense...
, which is fundamental to the stochastic calculus of variationsCalculus of variationsCalculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
(Malliavin calculusMalliavin calculusThe Malliavin calculus, named after Paul Malliavin, is a theory of variational stochastic calculus. In other words it provides the mechanics to compute derivatives of random variables....
); - δ is an infinite-dimensional generalization of the divergenceDivergenceIn vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
operator from classical vector calculus.
Preliminaries: the Malliavin derivative
Consider a fixed probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
(Ω, Σ, P) and a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H; E denotes expectation
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
with respect to P:
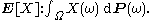
Intuitively speaking, the Malliavin derivative of a random variable F in Lp(Ω) is defined by expanding it in terms of Gaussian random variables that are parametrized by the elements of H and differentiating the expansion formally; the Skorokhod integral is the adjoint operation to the Malliavin derivative.
Consider a family of R-valued random variables W(h), indexed by the elements h of the Hilbert space H. Assume further that each W(h) is a Gaussian (normal) random variable, that the map taking h to W(h) is a linear map, and that the mean
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
and covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
structure is given by
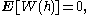
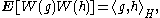
for all g and h in H. It can be shown that, given H, there always exists a probability space (Ω, Σ, P) and a family of random variables with the above properties. The Malliavin derivative is essentially defined by formally setting the derivative of the random variable W(h) to be h, and then extending this definition to “smooth enough
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
” random variables. For a random variable F of the form
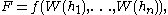
where f : Rn → R is smooth, the Malliavin derivative is defined using the earlier “formal definition” and the chain rule:
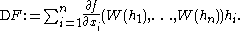
In other words, whereas F was a real-valued random variable, its derivative DF is an H-valued random variable, an element of the space Lp(Ω;H). Of course, this procedure only defines DF for “smooth” random variables, but an approximation procedure can be employed to define DF for F in a large subspace of Lp(Ω); the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of D is the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of the smooth random variables in the seminorm
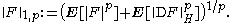
This space is denoted by D1,p and is called the Watanabe-Sobolev space.
The Skorokhod integral
For simplicity, consider now just the case p = 2. The Skorokhod integral δ is defined to be the L2-adjoint of the Malliavin derivative D. Just as D was not defined on the whole of L2(Ω), δ is not defined on the whole of L2(Ω; H): the domain of δ consists of those processes u in L2(Ω; H) for which there exists a constant C(u) such that, for all F in D1,2,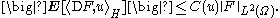
The Skorokhod integral of a process u in L2(Ω; H) is a real-valued random variable δu in L2(Ω); if u lies in the domain of δ, then δu is defined by the relation that, for all F ∈ D1,2,

Just as the Malliavin derivative D was first defined on simple, smooth random variables, the Skorokhod integral has a simple expression for “simple processes”: if u is given by

with Fj smooth and hj in H, then
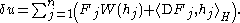
Properties
- The isometryIsometryIn mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
property: for any process u in L2(Ω; H) that lies in the domain of δ,
- If u is an adapted process, then the second term on the right-hand side is zero, the Skorokhod and Itō integrals coincide, and the above equation becomes the Itō isometryIto isometryIn mathematics, the Itō isometry, named after Kiyoshi Itō, is a crucial fact about Itō stochastic integrals. One of its main applications is to enable the computation of variances for stochastic processes....
.
- The derivative of a Skorokhod integral is given by the formula
- where DhX stands for (DX)(h), the random variable that is the value of the process DX at “time” h in H.
- The Skorokhod integral of the product of a random variable F in D1,2 and a process u in dom(δ) is given by the formula