
Smoothing spline
Encyclopedia
The smoothing spline is a method of smoothing
(fitting a smooth curve to a set of noisy observations) using a spline function.
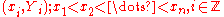 be a sequence of observations, modeled by the relation
be a sequence of observations, modeled by the relation  . The smoothing spline estimate
. The smoothing spline estimate 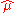 of the function
of the function  is defined to be the minimizer (over the class of twice differentiable functions) of
is defined to be the minimizer (over the class of twice differentiable functions) of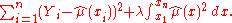
Remarks:
Now, treat the second step first.
Given the vector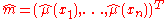 of fitted values, the sum-of-squares part of the spline criterion is fixed. It remains only to minimize
of fitted values, the sum-of-squares part of the spline criterion is fixed. It remains only to minimize 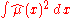 , and the minimizer is a natural cubic spline
, and the minimizer is a natural cubic spline
that interpolates the points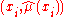 . This interpolating spline is a linear operator, and can be written in the form
. This interpolating spline is a linear operator, and can be written in the form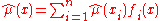
where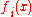 are a set of spline basis functions. As a result, the roughness penalty has the form
are a set of spline basis functions. As a result, the roughness penalty has the form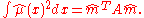
where the elements of A are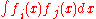 . The basis functions, and hence the matrix A, depend on the configuration of the predictor variables
. The basis functions, and hence the matrix A, depend on the configuration of the predictor variables 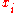 , but not on the responses
, but not on the responses  or
or  .
.
Now back the first step. The penalized sum-of-squares can be written as
where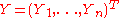 .
.
Minimizing over gives
gives
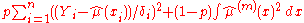
where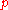 is a parameter called smooth factor and belongs to the interval
is a parameter called smooth factor and belongs to the interval 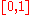 , and
, and  are the quantities controlling the extent of smoothing (they represent the weight
are the quantities controlling the extent of smoothing (they represent the weight 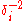 of each point
of each point  ). In practice, since cubic splines are mostly used,
). In practice, since cubic splines are mostly used,  is usually
is usually 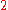 . The solution for
. The solution for  was proposed by Reinsch in 1967. For
was proposed by Reinsch in 1967. For  , when
, when 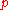 approaches
approaches 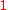 ,
, 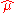 converges to the "natural" spline interpolant to the given data. As
converges to the "natural" spline interpolant to the given data. As 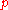 approaches
approaches  ,
, 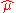 converges to a straight line (the smoothest curve). Since finding a suitable value of
converges to a straight line (the smoothest curve). Since finding a suitable value of 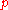 is a task of trial and error, a redundant constant
is a task of trial and error, a redundant constant 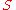 was introduced for convenience.
was introduced for convenience.
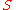 is used to numerically determine the value of
is used to numerically determine the value of 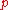 so that the function
so that the function 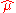 meets the following condition:
meets the following condition:
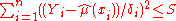
The algorithm described by de Boor starts with and increases
and increases 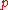 until the condition is met.. If
until the condition is met.. If 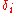 is an estimation of the standard deviation for
is an estimation of the standard deviation for  , the constant
, the constant 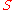 is recommended to be chosen in the interval
is recommended to be chosen in the interval 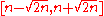 . Having
. Having  means the solution is the "natural" spline interpolant. Increasing
means the solution is the "natural" spline interpolant. Increasing 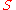 means we obtain a smoother curve by getting farther from the given data.
means we obtain a smoother curve by getting farther from the given data.
 we can conclude that the algorithm doesn't work for any sets of data. If we plan to use this algorithm for random points in a multidimensional space we need to find a solution to give as input to the algorithm sets of data where these constraints are met. A solution for this is to introduce a parameter so that the input data would be represented as single-valued functions depending on that parameter; after this the smoothing will be performed for each function. In a bidimensional space a solution would be to parametrize
we can conclude that the algorithm doesn't work for any sets of data. If we plan to use this algorithm for random points in a multidimensional space we need to find a solution to give as input to the algorithm sets of data where these constraints are met. A solution for this is to introduce a parameter so that the input data would be represented as single-valued functions depending on that parameter; after this the smoothing will be performed for each function. In a bidimensional space a solution would be to parametrize  and
and 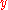 so that they would become
so that they would become 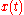 and
and 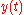 where
where 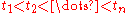 . A convenient solution for
. A convenient solution for  is the cumulating distance
is the cumulating distance 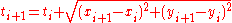 where
where  .
.
A more detailed analysis on parametrization is done by E.T.Y Lee.
smoothing can be found in the examples from Carl de Boor's
book A Practical Guide to Splines. The examples are in Fortran
programming language
. The updated sources are available also on Carl de Boor's official sitehttp://pages.cs.wisc.edu/~deboor/.
Smoothing
In statistics and image processing, to smooth a data set is to create an approximating function that attempts to capture important patterns in the data, while leaving out noise or other fine-scale structures/rapid phenomena. Many different algorithms are used in smoothing...
(fitting a smooth curve to a set of noisy observations) using a spline function.
Definition
Let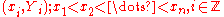 be a sequence of observations, modeled by the relation
be a sequence of observations, modeled by the relation  . The smoothing spline estimate
. The smoothing spline estimate 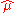 of the function
of the function  is defined to be the minimizer (over the class of twice differentiable functions) of
is defined to be the minimizer (over the class of twice differentiable functions) of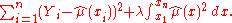
Remarks:
-
 is a smoothing parameter, controlling the trade-off between fidelity to the data and roughness of the function estimate.
is a smoothing parameter, controlling the trade-off between fidelity to the data and roughness of the function estimate. - The integral is evaluated over the range of the
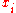 .
. - As
 (no smoothing), the smoothing spline converges to the interpolating spline.
(no smoothing), the smoothing spline converges to the interpolating spline. - As
 (infinite smoothing), the roughness penalty becomes paramount and the estimate converges to a linear least squaresLinear least squaresIn statistics and mathematics, linear least squares is an approach to fitting a mathematical or statistical model to data in cases where the idealized value provided by the model for any data point is expressed linearly in terms of the unknown parameters of the model...
(infinite smoothing), the roughness penalty becomes paramount and the estimate converges to a linear least squaresLinear least squaresIn statistics and mathematics, linear least squares is an approach to fitting a mathematical or statistical model to data in cases where the idealized value provided by the model for any data point is expressed linearly in terms of the unknown parameters of the model...
estimate. - The roughness penalty based on the second derivativeSecond derivativeIn calculus, the second derivative of a function ƒ is the derivative of the derivative of ƒ. Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, the second derivative of the position of a vehicle with respect to time is...
is the most common in modern statistics literature, although the method can easily be adapted to penalties based on other derivatives. - In early literature, with equally-spaced
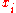 , second or third-order differences were used in the penalty, rather than derivatives.
, second or third-order differences were used in the penalty, rather than derivatives. - When the sum-of-squares term is replaced by a log-likelihood, the resulting estimate is termed penalized likelihood. The smoothing spline is the special case of penalized likelihood resulting from a Gaussian likelihood.
Derivation of the smoothing spline
It is useful to think of fitting a smoothing spline in two steps:- First, derive the values
 .
. - From these values, derive
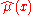 for all x.
for all x.
Now, treat the second step first.
Given the vector
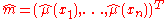 of fitted values, the sum-of-squares part of the spline criterion is fixed. It remains only to minimize
of fitted values, the sum-of-squares part of the spline criterion is fixed. It remains only to minimize 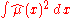 , and the minimizer is a natural cubic spline
, and the minimizer is a natural cubic splineSpline (mathematics)
In mathematics, a spline is a sufficiently smooth piecewise-polynomial function. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low-degree polynomials, while avoiding Runge's phenomenon for higher...
that interpolates the points
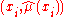 . This interpolating spline is a linear operator, and can be written in the form
. This interpolating spline is a linear operator, and can be written in the form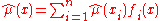
where
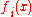 are a set of spline basis functions. As a result, the roughness penalty has the form
are a set of spline basis functions. As a result, the roughness penalty has the form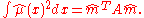
where the elements of A are
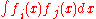 . The basis functions, and hence the matrix A, depend on the configuration of the predictor variables
. The basis functions, and hence the matrix A, depend on the configuration of the predictor variables 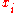 , but not on the responses
, but not on the responses  or
or  .
.Now back the first step. The penalized sum-of-squares can be written as

where
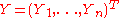 .
.Minimizing over
 gives
gives
De Boor's approach
De Boor's approach exploits the same idea, of finding a balance between having a smooth curve and being close to the given data.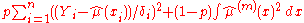
where
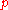 is a parameter called smooth factor and belongs to the interval
is a parameter called smooth factor and belongs to the interval 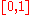 , and
, and  are the quantities controlling the extent of smoothing (they represent the weight
are the quantities controlling the extent of smoothing (they represent the weight 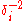 of each point
of each point  ). In practice, since cubic splines are mostly used,
). In practice, since cubic splines are mostly used,  is usually
is usually 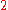 . The solution for
. The solution for  was proposed by Reinsch in 1967. For
was proposed by Reinsch in 1967. For  , when
, when 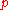 approaches
approaches 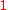 ,
, 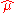 converges to the "natural" spline interpolant to the given data. As
converges to the "natural" spline interpolant to the given data. As 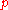 approaches
approaches  ,
, 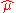 converges to a straight line (the smoothest curve). Since finding a suitable value of
converges to a straight line (the smoothest curve). Since finding a suitable value of 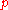 is a task of trial and error, a redundant constant
is a task of trial and error, a redundant constant 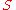 was introduced for convenience.
was introduced for convenience.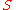 is used to numerically determine the value of
is used to numerically determine the value of 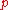 so that the function
so that the function 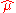 meets the following condition:
meets the following condition: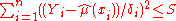
The algorithm described by de Boor starts with
 and increases
and increases 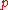 until the condition is met.. If
until the condition is met.. If 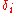 is an estimation of the standard deviation for
is an estimation of the standard deviation for  , the constant
, the constant 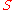 is recommended to be chosen in the interval
is recommended to be chosen in the interval 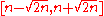 . Having
. Having  means the solution is the "natural" spline interpolant. Increasing
means the solution is the "natural" spline interpolant. Increasing 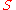 means we obtain a smoother curve by getting farther from the given data.
means we obtain a smoother curve by getting farther from the given data.Creating a multidimensional spline
Given the constraint from the definition formula we can conclude that the algorithm doesn't work for any sets of data. If we plan to use this algorithm for random points in a multidimensional space we need to find a solution to give as input to the algorithm sets of data where these constraints are met. A solution for this is to introduce a parameter so that the input data would be represented as single-valued functions depending on that parameter; after this the smoothing will be performed for each function. In a bidimensional space a solution would be to parametrize
we can conclude that the algorithm doesn't work for any sets of data. If we plan to use this algorithm for random points in a multidimensional space we need to find a solution to give as input to the algorithm sets of data where these constraints are met. A solution for this is to introduce a parameter so that the input data would be represented as single-valued functions depending on that parameter; after this the smoothing will be performed for each function. In a bidimensional space a solution would be to parametrize  and
and 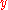 so that they would become
so that they would become 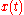 and
and 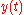 where
where 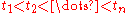 . A convenient solution for
. A convenient solution for  is the cumulating distance
is the cumulating distance 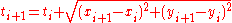 where
where  .
.A more detailed analysis on parametrization is done by E.T.Y Lee.
Related methods
Smoothing splines are related to, but distinct from:- Regression splines. In this method, the data is fitted to a set of spline basis functions with a reduced set of knots, typically by least squares. No roughness penalty is used.
- Penalized Splines. This combines the reduced knots of regression splines, with the roughness penalty of smoothing splines.
- Elastic mapElastic mapElastic maps provide a tool for nonlinear dimensionality reduction. By their construction, they are system of elastic springs embedded in the dataspace. This system approximates a low-dimensional manifold...
s method for manifold learning. This method combines the least squaresLeast squaresThe method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
penalty for approximation error with the bending and stretching penalty of the approximating manifold and uses the coarse discretization of the optimization problem.
Source code
Source code for splineSpline (mathematics)
In mathematics, a spline is a sufficiently smooth piecewise-polynomial function. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low-degree polynomials, while avoiding Runge's phenomenon for higher...
smoothing can be found in the examples from Carl de Boor's
Carl R. de Boor
Carl-Wilhelm Reinhold de Boor is a German-American mathematician and professor emeritus at the University of Wisconsin–Madison.-Early life:...
book A Practical Guide to Splines. The examples are in Fortran
Fortran
Fortran is a general-purpose, procedural, imperative programming language that is especially suited to numeric computation and scientific computing...
programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
. The updated sources are available also on Carl de Boor's official sitehttp://pages.cs.wisc.edu/~deboor/.
Further reading
- Wahba, G. (1990). Spline Models for Observational Data. SIAM, Philadelphia.
- Green, P. J. and Silverman, B. W. (1994). Nonparametric Regression and Generalized Linear Models. CRC Press.
- De Boor, C. (2001). A Practical Guide to Splines (Revised Edition). Springer.

