
Solving the geodesic equations
Encyclopedia
Solving the geodesic equations is a procedure used in mathematics
, particularly Riemannian geometry
, and in physics
, particularly in general relativity
, that results in obtaining geodesic
s. Physically, these represent the paths of (usually ideal) particles with no proper acceleration
, their motion satisfying the geodesic equations. Because the particles are subject to no four-acceleration, the geodesics generally represent the straightest path between two points in a curved spacetime
.
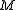 , the geodesic equation written in a coordinate chart with coordinates
, the geodesic equation written in a coordinate chart with coordinates 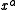 is:
is:
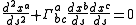
where the coordinates xa(s) are regarded as the coordinates of a curve
γ(s) in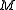 and
and 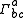 are the Christoffel symbols. The Christoffel symbols are functions of the metric
are the Christoffel symbols. The Christoffel symbols are functions of the metric
and are given by:
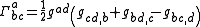
where the comma indicates a partial derivative
with respect to the coordinates:
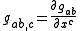
As the manifold has dimension , the geodesic equations are a system of
, the geodesic equations are a system of  ordinary differential equation
ordinary differential equation
s for the coordinate variables. Thus, allied with initial conditions, the system can, according to the Picard–Lindelöf theorem, be solved. One can also use a Lagrangian approach to the problem: defining
coordinate variables. Thus, allied with initial conditions, the system can, according to the Picard–Lindelöf theorem, be solved. One can also use a Lagrangian approach to the problem: defining
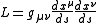
and applying the Euler-Lagrange equation
.
can be written in any coordinate system
, it is convenient to choose one that simplifies the geodesic equations. Mathematically, this means, a coordinate chart is chosen in which the geodesic equations have a particularly tractable form.
, the former may be consolidated into an effective potential dependent only on position. In this case, many of the heuristic
methods of analysing energy diagrams apply, in particular the location of turning points.
, possibly even the general solution, of the geodesic equations. Most attacks secretly employ the point symmetry group of the system of geodesic equations. This often yields a result giving a family of solutions implicitly, but in many examples does yield the general solution in explicit form.
In general relativity, to obtain timelike geodesics it is often simplest to start from the spacetime metric
, after dividing by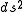 to obtain the form
to obtain the form
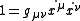
where the dot represents differentiation with respect to . Because timelike geodesics are maximal
. Because timelike geodesics are maximal
, one may apply the Euler-Lagrange equation
directly, and thus obtain a set of equations equivalent to the geodesic equations. This method has the advantage of bypassing a tedious calculation of Christoffel symbols
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, and in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, particularly in general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, that results in obtaining geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s. Physically, these represent the paths of (usually ideal) particles with no proper acceleration
Four-acceleration
In special relativity, four-acceleration is a four-vector and is defined as the change in four-velocity over the particle's proper time:whereandand \gamma_u is the Lorentz factor for the speed u...
, their motion satisfying the geodesic equations. Because the particles are subject to no four-acceleration, the geodesics generally represent the straightest path between two points in a curved spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
.
The geodesic equation
On an n-dimensional Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
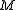 , the geodesic equation written in a coordinate chart with coordinates
, the geodesic equation written in a coordinate chart with coordinates 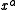 is:
is: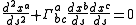
where the coordinates xa(s) are regarded as the coordinates of a curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
γ(s) in
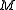 and
and 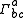 are the Christoffel symbols. The Christoffel symbols are functions of the metric
are the Christoffel symbols. The Christoffel symbols are functions of the metricMetric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
and are given by:
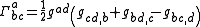
where the comma indicates a partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
with respect to the coordinates:
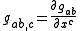
As the manifold has dimension
 , the geodesic equations are a system of
, the geodesic equations are a system of  ordinary differential equation
ordinary differential equationOrdinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s for the
 coordinate variables. Thus, allied with initial conditions, the system can, according to the Picard–Lindelöf theorem, be solved. One can also use a Lagrangian approach to the problem: defining
coordinate variables. Thus, allied with initial conditions, the system can, according to the Picard–Lindelöf theorem, be solved. One can also use a Lagrangian approach to the problem: defining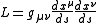
and applying the Euler-Lagrange equation
Euler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
.
Heuristics
As the laws of physicsPhysical law
A physical law or scientific law is "a theoretical principle deduced from particular facts, applicable to a defined group or class of phenomena, and expressible by the statement that a particular phenomenon always occurs if certain conditions be present." Physical laws are typically conclusions...
can be written in any coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
, it is convenient to choose one that simplifies the geodesic equations. Mathematically, this means, a coordinate chart is chosen in which the geodesic equations have a particularly tractable form.
Effective potentials
When the geodesic equations can be separated into terms containing only an undifferentiated variable and terms containing only its derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
, the former may be consolidated into an effective potential dependent only on position. In this case, many of the heuristic
Heuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
methods of analysing energy diagrams apply, in particular the location of turning points.
Solution techniques
Solving the geodesic equations means obtaining an exact solutionExact solution
In mathematics and especially physics, an exact solution is a solution to a problem that encapsulates the whole mathematics or physics of the problem without using an approximation.-References:*...
, possibly even the general solution, of the geodesic equations. Most attacks secretly employ the point symmetry group of the system of geodesic equations. This often yields a result giving a family of solutions implicitly, but in many examples does yield the general solution in explicit form.
In general relativity, to obtain timelike geodesics it is often simplest to start from the spacetime metric
Metric tensor (general relativity)
In general relativity, the metric tensor is the fundamental object of study. It may loosely be thought of as a generalization of the gravitational field familiar from Newtonian gravitation...
, after dividing by
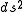 to obtain the form
to obtain the form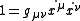
where the dot represents differentiation with respect to
 . Because timelike geodesics are maximal
. Because timelike geodesics are maximalMaximal element
In mathematics, especially in order theory, a maximal element of a subset S of some partially ordered set is an element of S that is not smaller than any other element in S. The term minimal element is defined dually...
, one may apply the Euler-Lagrange equation
Euler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
directly, and thus obtain a set of equations equivalent to the geodesic equations. This method has the advantage of bypassing a tedious calculation of Christoffel symbols
Christoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
.
See also
- Geodesics of the Schwarzschild vacuum
- Mathematics of general relativityMathematics of general relativityThe mathematics of general relativity refers to various mathematical structures and techniques that are used in studying and formulating Albert Einstein's theory of general relativity. The main tools used in this geometrical theory of gravitation are tensor fields defined on a Lorentzian manifold...
- Transition from special relativity to general relativity

