
Solvmanifold
Encyclopedia
In mathematics
, a solvmanifold is a homogeneous space
of a connected solvable Lie group. It may also be characterized as a quotient of a connected solvable Lie group by a closed subgroup
. (Some authors also require that the Lie group be simply-connected, or that the quotient be compact.)
A special class of solvmanifolds, nilmanifold
s, was introduced by Malcev, who proved first structural theorems. Properties of general solvmanifolds are similar, but somewhat more complicated.
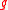 be a real Lie algebra
be a real Lie algebra
. It is called a complete Lie algebra if each map
in its adjoint representation is hyperbolic, i.e. has real eigenvalues. Let G be a solvable Lie group whose Lie algebra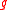 is complete. Then for any closed subgroup Γ of G, the solvmanifold G/Γ is a complete solvmanifold.
is complete. Then for any closed subgroup Γ of G, the solvmanifold G/Γ is a complete solvmanifold.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a solvmanifold is a homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
of a connected solvable Lie group. It may also be characterized as a quotient of a connected solvable Lie group by a closed subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
. (Some authors also require that the Lie group be simply-connected, or that the quotient be compact.)
A special class of solvmanifolds, nilmanifold
Nilmanifold
In mathematics, a nilmanifold is a differentiable manifold which has a transitive nilpotent group of diffeomorphisms acting on it. As such, a nilmanifold is an example of a homogeneous space and is diffeomorphic to the quotient space N/H, the quotient of a nilpotent Lie group N modulo a closed...
s, was introduced by Malcev, who proved first structural theorems. Properties of general solvmanifolds are similar, but somewhat more complicated.
Examples
- A solvable Lie group is trivially a solvmanifold.
- Every nilpotent groupNilpotent groupIn mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
is solvable, therefore, every nilmanifoldNilmanifoldIn mathematics, a nilmanifold is a differentiable manifold which has a transitive nilpotent group of diffeomorphisms acting on it. As such, a nilmanifold is an example of a homogeneous space and is diffeomorphic to the quotient space N/H, the quotient of a nilpotent Lie group N modulo a closed...
is a solvmanifold. This class of examples includes n-dimensional toriTorusIn geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
and the quotient of the 3-dimensional real Heisenberg group by its integral Heisenberg subgroup.
- The Möbius bandMobius BandMobius Band is an electronic rock trio from Brooklyn, New York consisting of Noam Schatz , Peter Sax , and Ben Sterling .-History:...
and the Klein bottleKlein bottleIn mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
are solvmanifolds that are not nilmanifolds.
- The mapping torusMapping torusIn mathematics, the mapping torus in topology of a homeomorphism f of some topological space X to itself is a particular geometric construction with f...
of an Anosov diffeomorphismAnosov diffeomorphismIn mathematics, more particularly in the fields of dynamical systems and geometric topology, an Anosov map on a manifold M is a certain type of mapping, from M to itself, with rather clearly marked local directions of 'expansion' and 'contraction'. Anosov systems are a special case of Axiom A...
of the n-torus is a solvmanifold. For n=2, these manifolds belong to Sol, one of the eight Thurston geometries.
Properties
- A solvmanifold is diffeomorphic to the total space of a vector bundleVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
over some compact solvmanifold. This statement was conjectured by G. MostowGeorge MostowGeorge Mostow is an American mathematician, a member of the National Academy of Sciences, Henry Ford II Professor of Mathematics at Yale University, the 49th President of the American Mathematical Society ,...
and proved by L. AuslanderLouis AuslanderLouis Auslander was an American mathematician. He had wide ranging interests both in pure and applied mathematics and worked on Finsler geometry, geometry of solvmanifolds and nilmanifolds, locally affine spaces, many aspects of harmonic analysis, representation theory of solvable Lie groups, and...
and R. Tolimieri.
- The fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of an arbitrary solvmanifold is policyclicPolycyclic groupIn mathematics, a polycyclic group is a solvable group that satisfies the maximal condition on subgroups...
.
- A compact solvmanifold is determined up to diffeomorphism by its fundamental group.
- Fundamental groups of compact solvmanifolds may be characterized as group extensionGroup extensionIn mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence...
s of free abelian groupFree abelian groupIn abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
s of finite rank by finitely generated torsion-free nilpotent groups.
- Every solvmanifold is asphericalAsphericalAspherical may refer to:* Aspherical space, a concept in topology* Aspherical lens, a type of lens assembly used in photography which contains an aspheric lens...
. Among all compact homogeneous spaces, solvmanifolds may be characterized by the properties of being aspherical and having a solvable fundamental group.
Odd section
Let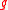 be a real Lie algebra
be a real Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
. It is called a complete Lie algebra if each map
- ad
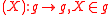
in its adjoint representation is hyperbolic, i.e. has real eigenvalues. Let G be a solvable Lie group whose Lie algebra
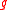 is complete. Then for any closed subgroup Γ of G, the solvmanifold G/Γ is a complete solvmanifold.
is complete. Then for any closed subgroup Γ of G, the solvmanifold G/Γ is a complete solvmanifold.

