Source coding
Encyclopedia
In information theory
, Shannon's source coding theorem (or noiseless coding theorem) establishes the limits to possible data compression
, and the operational meaning of the Shannon entropy.
The source coding theorem shows that (in the limit, as the length of a stream of independent and identically-distributed random variable (i.i.d.) data tends to infinity) it is impossible to compress the data such that the code rate (average number of bits per symbol) is less than the Shannon entropy of the source, without it being virtually certain that information will be lost. However it is possible to get the code rate arbitrarily close to the Shannon entropy, with negligible probability of loss.
The source coding theorem for symbol codes places an upper and a lower bound on the minimal possible expected length of codewords as a function of the entropy of the input word (which is viewed as a random variable
) and of the size of the target alphabet.
.
, 
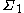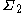denote two finite alphabets and let 
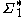and 
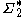denote the set of all finite words
from those alphabets (respectively).
Suppose that X is a random variable taking values in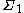
and let f be a uniquely decodable code from 
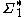to 
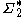where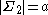 
. Let S denote the random variable given by the wordlength f(X).
If f is optimal in the sense that it has the minimal expected wordlength for X, then
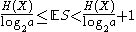
(Shannon 1948)
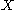is an i.i.d. source, its time series
X1, ..., Xn is i.i.d. with entropy
H(X) in the discrete-valued case and differential entropy
in the continuous-valued case. The Source coding theorem states that for any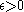
for any rate larger than the entropy
of the source, there is large enough
and an encoder that takes 
i.i.d. repetition of the source,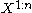 
, and maps it to 
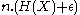binary bits such that the source symbols 
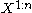are recoverable from the binary bits with probability at least 
.
Proof for achievability
Fix some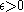
. The typical set,
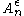, is defined as follows:
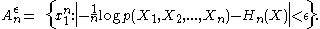
AEP shows that for large enough n, the probability that a sequence generated by the source lies in the typical set,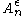
, as defined approaches one. In particular there for large enough n, 
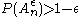(See
AEP for a proof):
The definition of typical sets implies that those sequences that lie in the typical set satisfy:
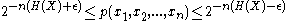
Note that:
Since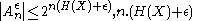
bits are enough to point to any string in this set.
The encoding algorithm: The encoder checks if the input sequence lies within the typical set; if yes, it outputs the index of the input sequence within the typical set; if not, the encoder outputs an arbitrary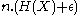
digit number. As long as the input sequence lies within the typical set (with probability at least 
), the encoder doesn't make any error. So, the probability of error of the encoder is bounded above by 
Proof for converse
The converse is proved by showing that any set of size smaller than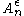
(in the sense of exponent) would cover a set of probability bounded away from 1.
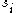denote the wordlength of each possible 
(
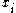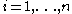). Define 
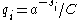, where C is chosen so that 
.
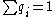Then
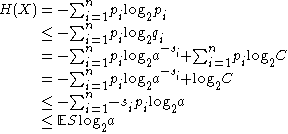
where the second line follows from Gibbs' inequality
and the fifth line follows from Kraft's inequality
:
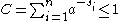so 
.
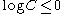For the second inequality we may set
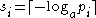
so that
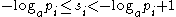
and so
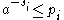
and
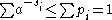
and so by Kraft's inequality there exists a prefix-free code having those wordlengths. Thus the minimal S satisfies
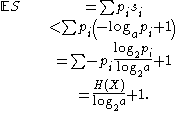
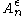as:
Then, for given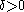
, for n large enough, 
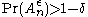. Now we just encode the sequences in the typical set, and usual methods in source coding show that the cardinality of this set is smaller than 
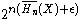. Thus, on an average, 
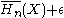bits suffice for encoding with probability greater than 
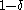, where 
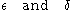can be made arbitrarily small, by making n larger.
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, Shannon's source coding theorem (or noiseless coding theorem) establishes the limits to possible data compression
Data compression
In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
, and the operational meaning of the Shannon entropy.
The source coding theorem shows that (in the limit, as the length of a stream of independent and identically-distributed random variable (i.i.d.) data tends to infinity) it is impossible to compress the data such that the code rate (average number of bits per symbol) is less than the Shannon entropy of the source, without it being virtually certain that information will be lost. However it is possible to get the code rate arbitrarily close to the Shannon entropy, with negligible probability of loss.
The source coding theorem for symbol codes places an upper and a lower bound on the minimal possible expected length of codewords as a function of the entropy of the input word (which is viewed as a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
) and of the size of the target alphabet.
Statements
Source coding is a mapping from (a sequence of) symbols from an information source to a sequence of alphabet symbols (usually bits) such that the source symbols can be exactly recovered from the binary bits (lossless source coding) or recovered within some distortion (lossy source coding). This is the concept behind data compressionData compression
In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
.
Source coding theorem
In information theory, the source coding theorem (Shannon 1948) informally states that:- "N i.i.d. random variables each with entropyInformation entropyIn information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
H(X) can be compressed into more than N H(X) bitsBITSBITS or bits may refer to:* Plural of bit* Background Intelligent Transfer Service, a file transfer protocol* Birla Institute of Technology and Science, a technology school in Pilani, Rajasthan, India, with campuses in Goa, Hyderabad, and Dubai...
with negligible risk of information loss, as N tends to infinity; but conversely, if they are compressed into fewer than N H(X) bits it is virtually certain that information will be lost." (MacKay 2003, pg. 81,Cover:Chapter 5).
Source coding theorem for symbol codes
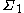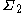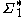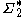Let, denote two finite alphabets and let and denote the set of all finite wordsKleene star
In mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
from those alphabets (respectively).
Suppose that X is a random variable taking values in
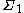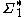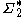and let f be a uniquely decodable code from to where 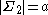. Let S denote the random variable given by the wordlength f(X).If f is optimal in the sense that it has the minimal expected wordlength for X, then
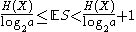
(Shannon 1948)
Proof: Source coding theorem
Given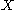 is an i.i.d. source, its time seriesTime series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
X1, ..., Xn is i.i.d. with entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
H(X) in the discrete-valued case and differential entropy
Differential entropy
Differential entropy is a concept in information theory that extends the idea of entropy, a measure of average surprisal of a random variable, to continuous probability distributions.-Definition:...
in the continuous-valued case. The Source coding theorem states that for any
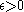for any rate larger than the entropyEntropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
of the source, there is large enough
and an encoder that takes i.i.d. repetition of the source, 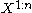, and maps it to 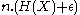binary bits such that the source symbols 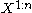are recoverable from the binary bits with probability at least .Proof for achievability
Fix some
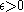. The typical set,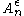, is defined as follows: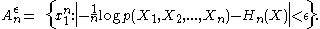AEP shows that for large enough n, the probability that a sequence generated by the source lies in the typical set,
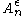, as defined approaches one. In particular there for large enough n, 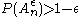(SeeAEP for a proof):
The definition of typical sets implies that those sequences that lie in the typical set satisfy:
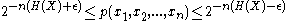
Note that:
- The probability of a sequence from
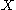being drawn from 
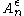is greater than 
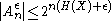since the probability of the whole set 
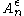is at most one.
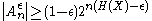. For the proof, use the upper bound on the probability of each term in typical set and the lower bound on the probability of the whole set 
.
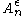Since
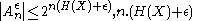bits are enough to point to any string in this set.The encoding algorithm: The encoder checks if the input sequence lies within the typical set; if yes, it outputs the index of the input sequence within the typical set; if not, the encoder outputs an arbitrary
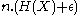digit number. As long as the input sequence lies within the typical set (with probability at least ), the encoder doesn't make any error. So, the probability of error of the encoder is bounded above by Proof for converse
The converse is proved by showing that any set of size smaller than
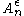(in the sense of exponent) would cover a set of probability bounded away from 1.Proof: Source coding theorem for symbol codes
Let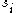 denote the wordlength of each possible 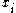(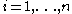). Define 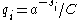, where C is chosen so that 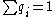.Then
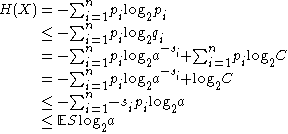
where the second line follows from Gibbs' inequality
Gibbs' inequality
In information theory, Gibbs' inequality is a statement about the mathematical entropy of a discrete probability distribution. Several other bounds on the entropy of probability distributions are derived from Gibbs' inequality, including Fano's inequality....
and the fifth line follows from Kraft's inequality
Kraft's inequality
In coding theory, Kraft's inequality, named after Leon Kraft, gives a necessary and sufficient condition for the existence of a uniquely decodable code for a given set of codeword lengths...
:
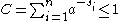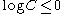so .For the second inequality we may set
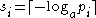
so that
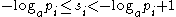
and so
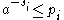
and
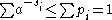
and so by Kraft's inequality there exists a prefix-free code having those wordlengths. Thus the minimal S satisfies
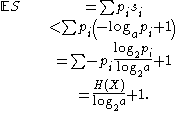
Fixed Rate lossless source coding for discrete time non-stationary independent sources
Define typical set as:
Then, for given
, for n large enough, 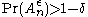. Now we just encode the sequences in the typical set, and usual methods in source coding show that the cardinality of this set is smaller than 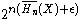. Thus, on an average, 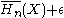bits suffice for encoding with probability greater than 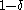, where 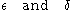can be made arbitrarily small, by making n larger.See also
- Channel coding
- Noisy Channel Coding TheoremNoisy channel coding theoremIn information theory, the noisy-channel coding theorem , establishes that for any given degree of noise contamination of a communication channel, it is possible to communicate discrete data nearly error-free up to a computable maximum rate through the channel...
- Error exponentError exponentIn information theory, the error exponent of a channel code or source code over the block length of the code is the logarithm of the error probability. For example, if the probability of error of a decoder drops as e–nα, where n is the block length, the error exponent is α...
- Asymptotic Equipartition PropertyAsymptotic equipartition propertyIn information theory the asymptotic equipartition property is a general property of the output samples of a stochastic source. It is fundamental to the concept of typical set used in theories of compression....
(AEP)