
Sparse language
Encyclopedia
In computational complexity theory
, a sparse language is a formal language
(a set of strings
) such that the number of strings of length n in the language is bounded by a polynomial
function of n. They are used primarily in the study of the relationship of the complexity class NP
with other classes. The complexity class
of all sparse languages is called SPARSE.
Sparse languages are called sparse because there are a total of 2n strings of length n, and if a language only contains polynomially many of these, then the proportion of strings of length n that it contains rapidly goes to zero as n grows. All unary languages are sparse. An example of a nontrivial sparse language is the set of binary strings containing exactly k 1 bits for some fixed k; for each n, there are only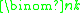
strings in the language, which is bounded by nk.
are sparse, there is a polynomial-time Turing reduction from any language in P/poly to a sparse language. Fortune showed in 1979 that if any sparse language is co-NP-complete
, then P = NP; Mahaney used this to show in 1982 that if any sparse language is NP-complete
, then P = NP (this is Mahaney's theorem). A simpler proof of this based on left-sets was given by Ogihara and Osamu in 1991. E
≠ NE
if and only if there exist sparse languages in NP that are not in P. In 1999, Jin-Yi Cai and D. Sivakumar, building on work by Ogihara, showed that if there exists a sparse P-complete
problem, then L
= P
.
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, a sparse language is a formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
(a set of strings
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
) such that the number of strings of length n in the language is bounded by a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
function of n. They are used primarily in the study of the relationship of the complexity class NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
with other classes. The complexity class
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
of all sparse languages is called SPARSE.
Sparse languages are called sparse because there are a total of 2n strings of length n, and if a language only contains polynomially many of these, then the proportion of strings of length n that it contains rapidly goes to zero as n grows. All unary languages are sparse. An example of a nontrivial sparse language is the set of binary strings containing exactly k 1 bits for some fixed k; for each n, there are only
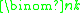
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
strings in the language, which is bounded by nk.
Relationships to other complexity classes
SPARSE contains TALLY, the class of unary languages, since these have at most one string of any one length. Although not all languages in P/polyP/poly
In computational complexity theory, P/poly is the complexity class of languages recognized by a polynomial-time Turing machine with a polynomial-bounded advice function. It is also equivalently defined as the class PSIZE of languages that have a polynomial-size circuits...
are sparse, there is a polynomial-time Turing reduction from any language in P/poly to a sparse language. Fortune showed in 1979 that if any sparse language is co-NP-complete
Co-NP-complete
In complexity theory, computational problems that are co-NP-complete are those that are the hardest problems in co-NP, in the sense that they are the ones most likely not to be in P...
, then P = NP; Mahaney used this to show in 1982 that if any sparse language is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
, then P = NP (this is Mahaney's theorem). A simpler proof of this based on left-sets was given by Ogihara and Osamu in 1991. E
E (complexity)
In computational complexity theory, the complexity class E is the set of decision problems that can be solved by a deterministic Turing machine in time 2O and is therefore equal to the complexity class DTIME....
≠ NE
NE (complexity)
In computational complexity theory, the complexity class NE is the set of decision problems that can be solved by a non-deterministic Turing machine in time O for some k....
if and only if there exist sparse languages in NP that are not in P. In 1999, Jin-Yi Cai and D. Sivakumar, building on work by Ogihara, showed that if there exists a sparse P-complete
P-complete
In complexity theory, the notion of P-complete decision problems is useful in the analysis of both:# which problems are difficult to parallelize effectively, and;# which problems are difficult to solve in limited space....
problem, then L
L (complexity)
In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space...
= P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
.
External links
- Lance Fortnow. Favorite Theorems: Small Sets. April 18, 2006.
- Bill Gasarch. Sparse Sets (Tribute to Mahaney). June 29, 2007.

