
Splitting theorem
Encyclopedia
The splitting theorem is a classical theorem in Riemannian geometry
. It states that if a complete Riemannian manifold
M with Ricci curvature

has a straight line, i.e., a geodesic
γ such that
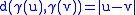
for all
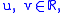
then it is isometric to a product space
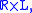
where is a Riemannian manifold with
is a Riemannian manifold with

The theorem was proved by Jeff Cheeger
and Detlef Gromoll
, based on an earlier result of Victor Andreevich Toponogov
, which required non-negative sectional curvature
.
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
. It states that if a complete Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
M with Ricci curvature
Ricci curvature
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume element of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space...

has a straight line, i.e., a geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
γ such that
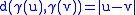
for all
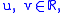
then it is isometric to a product space
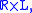
where
 is a Riemannian manifold with
is a Riemannian manifold with
The theorem was proved by Jeff Cheeger
Jeff Cheeger
Jeff Cheeger , is a mathematician. Cheeger is professor at the Courant Institute of Mathematical Sciences at New York University in New York City. His main interests are differential geometry and its applications to topology and analysis.-Biography:He graduated from Harvard University with a B.A....
and Detlef Gromoll
Detlef Gromoll
Detlef Gromoll was a mathematician who studied distortions of shapes in three or more dimensions. In his soul theorem, published in 1972, he and Jeff Cheeger studied the properties of surfaces that have flat regions or curves like the outside of a sphere but not regions shaped liked saddles...
, based on an earlier result of Victor Andreevich Toponogov
Victor Andreevich Toponogov
Victor Andreevich Toponogov was a Russian mathematician, noted for his contributions to differential geometry and so-called Riemannian geometry "in the large"....
, which required non-negative sectional curvature
Sectional curvature
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...
.

