
Square-free
Encyclopedia
In mathematics
, an element r of a unique factorization domain
R is called square-free if it is not divisible by a non-trivial square. That is, every s such that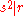 is a unit of R.
is a unit of R.
Square-free elements may be also characterized using their prime decomposition. The unique factorization property means that a non-zero non-unit r can be represented as a product of prime element
s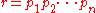
Then r is square-free if and only if the primes pi are pairwise non-associated (i.e. that it doesn't have two of the same prime as factors, which would make it divisible by a square number).
Common examples of square-free elements include square-free integer
s and square-free polynomial
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an element r of a unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
R is called square-free if it is not divisible by a non-trivial square. That is, every s such that
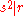 is a unit of R.
is a unit of R.Square-free elements may be also characterized using their prime decomposition. The unique factorization property means that a non-zero non-unit r can be represented as a product of prime element
Prime element
In abstract algebra, an element p of a commutative ring R is said to be prime if it is not zero, not a unit and whenever p divides ab for some a and b in R, then p divides a or p divides b...
s
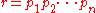
Then r is square-free if and only if the primes pi are pairwise non-associated (i.e. that it doesn't have two of the same prime as factors, which would make it divisible by a square number).
Common examples of square-free elements include square-free integer
Square-free integer
In mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...
s and square-free polynomial
Square-free polynomial
In mathematics, a square-free polynomial is a polynomial with no square factors, i.e, f \in F[x] is square-free if and only if b^2 \nmid f for every b \in F[x] with non-zero degree. This definition implies that no factors of higher order can exist, either, for if b3 divided the polynomial, then b2...
s.

