Squaring the square
Encyclopedia
Squaring the square is the problem of tiling
an integral square using only other integral squares. (An integral square is a square
whose sides have integer
length.) The name was coined in a humorous analogy with squaring the circle
. Squaring the square is an easy task unless additional conditions are set. The most studied restriction is that the squaring be perfect, meaning that the sizes of the smaller squares are all different. A related problem is squaring the plane, which can be done even with the restriction that each natural number occurs exactly once as a size of a square in the tiling.
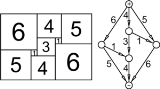
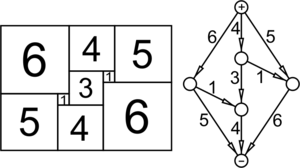A "perfect" squared square is a square such that each of the smaller squares has a different size.
It is first recorded as being studied by R. L. Brooks, C. A. B. Smith, A. H. Stone
and W. T. Tutte
at Cambridge University.
They transformed the square tiling into an equivalent electrical circuit — they called it "Smith diagram" — by considering the squares as resistor
s that connected to their neighbors at their top and bottom edges, and then applied Kirchhoff's circuit laws
and circuit decomposition techniques to that circuit.
The first perfect squared square was found by Roland Sprague in 1939.
If we take such a tiling and enlarge it so that the formerly smallest tile now has the size of the square S we started out from, then we see that we obtain from this a tiling of the plane with integral squares, each having a different size.
Martin Gardner
has published an extensive http://www.squaring.net/history_theory/brooks_smith_stone_tutte_II.html article written by W. T. Tutte
about the early history of squaring the square.
and P. Leeuw mathematically proved it to be the lowest-order example.
The smallest simple squared square forms the logo of the Trinity Mathematical Society
.
of all the smaller side lengths should be 1.
The Mrs. Perkins's quilt problem is to find a Mrs. Perkins's quilt with the fewest pieces for a given n × n square.
s without repetitions, which he called the heterogeneous tiling conjecture. This problem was later publicized by Martin Gardner in his Scientific American
column and appeared in several books, but it defied solution for over 30 years. In Tilings and Patterns, published in 1987, Branko Grünbaum
and G. C. Shephard stated that in all perfect integral tilings of the plane known at that time, the sizes of the squares grew exponentially
.
Recently, James Henle and Frederick Henle proved that this, in fact, can be done. Their proof is constructive and proceeds by "puffing up" an L
-shaped region formed by two side-by-side and horizontally flush squares of different sizes to a perfect tiling of a larger rectangular region, then adjoining the square of the smallest size not yet used to get another, larger L-shaped region. The squares added during the puffing up procedure have sizes that have not yet appeared in the construction and the procedure is set up so that the resulting rectangular regions are expanding in all four directions, which leads to a tiling of the whole plane.
C, the problem of dividing it into finitely many smaller cubes, no two congruent.
Unlike the case of squaring the square, a hard but solvable problem, cubing the cube is impossible. This can be shown by a relatively simple argument. Consider a hypothetical cubed cube. The bottom face of this cube is a squared square; lift off the rest of the cube, so you have a square region of the plane covered with a collection of cubes
Consider the smallest cube in this collection, with side c (call it S). Since the smallest square of a squared square cannot be on its edge, its neighbours will all tower over it, meaning that there isn't space to put a cube of side larger than c on top of it. Since the construction is a cubed cube, you're not allowed to use a cube of side equal to c; so only smaller cubes may stand upon S. This means that the top face of S must be a squared square, and the argument continues by infinite descent
. Thus it is not possible to dissect a cube into finitely many smaller cubes of different sizes.
Similarly, it is impossible to hypercube a hypercube, because each cell of the hypercube would need to be a cubed cube, and so on into the higher dimensions.
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
an integral square using only other integral squares. (An integral square is a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
whose sides have integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
length.) The name was coined in a humorous analogy with squaring the circle
Squaring the circle
Squaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge...
. Squaring the square is an easy task unless additional conditions are set. The most studied restriction is that the squaring be perfect, meaning that the sizes of the smaller squares are all different. A related problem is squaring the plane, which can be done even with the restriction that each natural number occurs exactly once as a size of a square in the tiling.
Perfect squared squares
It is first recorded as being studied by R. L. Brooks, C. A. B. Smith, A. H. Stone
Arthur Harold Stone
Arthur Harold Stone was a British mathematician born in London, who worked mostly in topology. His wife was American mathematician Dorothy Maharam...
and W. T. Tutte
W. T. Tutte
William Thomas Tutte, OC, FRS, known as Bill Tutte, was a British, later Canadian, codebreaker and mathematician. During World War II he made a brilliant and fundamental advance in Cryptanalysis of the Lorenz cipher, a major German code system, which had a significant impact on the Allied...
at Cambridge University.
They transformed the square tiling into an equivalent electrical circuit — they called it "Smith diagram" — by considering the squares as resistor
Resistor
A linear resistor is a linear, passive two-terminal electrical component that implements electrical resistance as a circuit element.The current through a resistor is in direct proportion to the voltage across the resistor's terminals. Thus, the ratio of the voltage applied across a resistor's...
s that connected to their neighbors at their top and bottom edges, and then applied Kirchhoff's circuit laws
Kirchhoff's circuit laws
Kirchhoff's circuit laws are two equalities that deal with the conservation of charge and energy in electrical circuits, and were first described in 1845 by Gustav Kirchhoff...
and circuit decomposition techniques to that circuit.
The first perfect squared square was found by Roland Sprague in 1939.
If we take such a tiling and enlarge it so that the formerly smallest tile now has the size of the square S we started out from, then we see that we obtain from this a tiling of the plane with integral squares, each having a different size.
Martin Gardner
Martin Gardner
Martin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...
has published an extensive http://www.squaring.net/history_theory/brooks_smith_stone_tutte_II.html article written by W. T. Tutte
W. T. Tutte
William Thomas Tutte, OC, FRS, known as Bill Tutte, was a British, later Canadian, codebreaker and mathematician. During World War II he made a brilliant and fundamental advance in Cryptanalysis of the Lorenz cipher, a major German code system, which had a significant impact on the Allied...
about the early history of squaring the square.
Simple squared squares
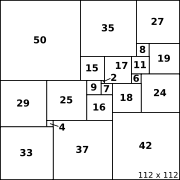
A "simple" squared square is one where no subset of the squares forms a rectangle or square, otherwise it is "compound". The smallest simple perfect squared square was discovered by A. J. W. Duijvestijn using a computer search. His tiling uses 21 squares, and has been proved to be minimal. The smallest perfect compound squared square was discovered by T.H. Willcocks in 1946 and has 24 squares; however, it was not until 1982 that Duijvestijn, Pasquale Joseph FedericoPasquale Joseph Federico
Pasquale Joseph Federico was a lifelong mathematician and longtime head of the United States Patent Office.-Biography:He was born in Monessen, Pennsylvania...
and P. Leeuw mathematically proved it to be the lowest-order example.
The smallest simple squared square forms the logo of the Trinity Mathematical Society
Trinity Mathematical Society
right|thumb|The [[squared square]] upon which the Trinity Mathematical Society logo is based.The Trinity Mathematical Society, abbreviated TMS, was founded in Trinity College, Cambridge in 1919 by G. H. Hardy to "promote the discussion of subjects of mathematical interest"...
.
Mrs. Perkins's quilt
When the constraint of all the squares being different sizes is relaxed, a squared square such that the side lengths of the smaller squares do not have a common divisor larger than 1 is called a "Mrs. Perkins's quilt". In other words, the greatest common divisorGreatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
of all the smaller side lengths should be 1.
The Mrs. Perkins's quilt problem is to find a Mrs. Perkins's quilt with the fewest pieces for a given n × n square.
Squaring the plane
In 1975, Solomon Golomb raised the question whether the whole plane can be tiled by squares whose sizes are all natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s without repetitions, which he called the heterogeneous tiling conjecture. This problem was later publicized by Martin Gardner in his Scientific American
Scientific American
Scientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
column and appeared in several books, but it defied solution for over 30 years. In Tilings and Patterns, published in 1987, Branko Grünbaum
Branko Grünbaum
Branko Grünbaum is a Croatian-born mathematician and a professor emeritus at the University of Washington in Seattle. He received his Ph.D. in 1957 from Hebrew University of Jerusalem in Israel....
and G. C. Shephard stated that in all perfect integral tilings of the plane known at that time, the sizes of the squares grew exponentially
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
.
Recently, James Henle and Frederick Henle proved that this, in fact, can be done. Their proof is constructive and proceeds by "puffing up" an L
L
Ł or ł, described in English as L with stroke, is a letter of the Polish, Kashubian, Sorbian, Łacinka , Łatynka , Wilamowicean, Navajo, Dene Suline, Inupiaq, Zuni, Hupa, and Dogrib alphabets, several proposed alphabets for the Venetian language, and the ISO 11940 romanization of the Thai alphabet...
-shaped region formed by two side-by-side and horizontally flush squares of different sizes to a perfect tiling of a larger rectangular region, then adjoining the square of the smallest size not yet used to get another, larger L-shaped region. The squares added during the puffing up procedure have sizes that have not yet appeared in the construction and the procedure is set up so that the resulting rectangular regions are expanding in all four directions, which leads to a tiling of the whole plane.
Cubing the cube
Cubing the cube is the analogue in three dimensions of squaring the square: that is, given a cubeCube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
C, the problem of dividing it into finitely many smaller cubes, no two congruent.
Unlike the case of squaring the square, a hard but solvable problem, cubing the cube is impossible. This can be shown by a relatively simple argument. Consider a hypothetical cubed cube. The bottom face of this cube is a squared square; lift off the rest of the cube, so you have a square region of the plane covered with a collection of cubes
Consider the smallest cube in this collection, with side c (call it S). Since the smallest square of a squared square cannot be on its edge, its neighbours will all tower over it, meaning that there isn't space to put a cube of side larger than c on top of it. Since the construction is a cubed cube, you're not allowed to use a cube of side equal to c; so only smaller cubes may stand upon S. This means that the top face of S must be a squared square, and the argument continues by infinite descent
Infinite descent
In mathematics, a proof by infinite descent is a particular kind of proof by contradiction which relies on the fact that the natural numbers are well ordered. One typical application is to show that a given equation has no solutions. Assuming a solution exists, one shows that another exists, that...
. Thus it is not possible to dissect a cube into finitely many smaller cubes of different sizes.
Similarly, it is impossible to hypercube a hypercube, because each cell of the hypercube would need to be a cubed cube, and so on into the higher dimensions.
External links
- Perfect squared squares:
- http://www.squaring.net/
- http://www.maa.org/editorial/mathgames/mathgames_12_01_03.html
- http://www.math.uwaterloo.ca/navigation/ideas/articles/honsberger2/index.shtml
- http://www.math.niu.edu/~rusin/known-math/98/square_dissect
- http://www.stat.ualberta.ca/people/schmu/preprints/sq.pdf
- Nowhere-neat squared squares:
- http://karl.kiwi.gen.nz/prosqtre.html
- Mrs. Perkins's quilt:
- Mrs. Perkins's Quilt on MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
- Mrs. Perkins's Quilt on MathWorld