St. Petersburg paradox
Encyclopedia
In economics
, the St. Petersburg paradox is a paradox
related to probability theory
and decision theory
. It is based on a particular (theoretical) lottery game (sometimes called St. Petersburg Lottery) that leads to a random variable
with infinite expected value
, i.e., infinite expected payoff, but would nevertheless be considered to be worth only a very small amount of money. The St. Petersburg paradox is a classical situation where a naïve decision criterion (which takes only the expected value into account) would recommend a course of action that no (real) rational
person would be willing to take. The paradox can be resolved when the decision model is refined via the notion of marginal utility
(and it is one origin of notions of utility
functions and of marginal utility), by taking into account the finite resources of the participants, or by noting that one simply cannot buy that which is not sold (and that sellers would not produce a lottery whose expected loss to them were unacceptable).
The paradox is named from Daniel Bernoulli
's presentation of the problem and his solution, published in 1738 in the Commentaries of the Imperial Academy of Science of Saint Petersburg
. However, the problem was invented by Daniel's cousin Nicolas Bernoulli
who first stated it in a letter to Pierre Raymond de Montmort
of 9 September 1713 .
: you pay a fixed fee to enter and then a fair coin is tossed
repeatedly until a tail appears, ending the game. The pot starts at 1 dollar and is doubled every time a head appears. You win whatever is in the pot after the game ends. Thus you win 1 dollar if a tail appears on the first toss, 2 dollars if a head appears on the first toss and a tail on the second, 4 dollars if a head appears on the first two tosses and a tail on the third, 8 dollars if a head appears on the first three tosses and a tail on the fourth, etc. In short, you win 2k−1 dollars if the coin is tossed k times until the first tail appears.
What would be a fair price to pay for entering the game? To answer this we need to consider what would be the average payout: With probability 1/2, you win 1 dollar; with probability 1/4 you win 2 dollars; with probability 1/8 you win 4 dollars etc. The expected value
is thus

This sum diverges to infinity, and so the expected win for the player of this game, at least in its idealized form, in which the casino has unlimited resources, is an infinite amount of money. This means that the player should almost surely
come out ahead in the long run, no matter how much he pays to enter; while a large payoff comes along very rarely, when it eventually does it will typically be far more than the amount of money that he has already paid to play. According to the usual treatment of deciding when it is advantageous and therefore rational to play, one should therefore play the game at any price if offered the opportunity. Yet, in published descriptions of the paradox, e.g., , many people expressed disbelief in the result.
Martin quotes Ian Hacking
as saying "few of us would pay even $25 to enter such a game" and says most commentators would agree.
, an expected utility hypothesis
, and the presumption of diminishing marginal utility of money.
In Daniel Bernoulli's own words:
A common utility model, suggested by Bernoulli himself, is the logarithmic function
u(w) = ln(w) (known as “log utility”). It is a function of the gambler’s total wealth w, and the concept of diminishing marginal utility of money is built into it. By the expected utility hypothesis, expected utilities can be calculated the same way expected values are. For each possible event, the change in utility ln(wealth after the event) - ln(wealth before the event) will be weighted by the probability of that event occurring. Let c be the cost charged to enter the game. The expected utility of the lottery now converges to a finite value:
This formula gives an implicit relationship between the gambler's wealth and how much he should be willing to pay to play (specifically, any c that gives a positive expected utility). For example, with log utility a millionaire should be willing to pay up to $10.94, a person with $1000 should pay up to $5.94, a person with $2 should pay up to $2, and a person with $0.60 should borrow $0.87 and pay up to $1.47.
Before Daniel Bernoulli published, in 1728, another Swiss mathematician, Gabriel Cramer
, had already found parts of this idea (also motivated by the St. Petersburg Paradox) in stating that
He demonstrated in a letter to Nicolas Bernoulli http://www.cs.xu.edu/math/Sources/Montmort/stpetersburg.pdf#search=%22Nicolas%20Bernoulli%22 that a square root function describing the diminishing marginal benefit of gains can resolve the problem. However, unlike Daniel Bernoulli, he did not consider the total wealth of a person, but only the gain by the lottery.
This solution by Cramer and Bernoulli, however, is not yet completely satisfying, since the lottery can easily be changed in a way such that the paradox reappears: To this aim, we just need to change the game so that it gives the (even larger) payoff . Again, the game should be worth an infinite amount. More generally, one can find a lottery that allows for a variant of the St. Petersburg paradox for every unbounded utility function, as was first pointed out by .
. Again, the game should be worth an infinite amount. More generally, one can find a lottery that allows for a variant of the St. Petersburg paradox for every unbounded utility function, as was first pointed out by .
There are basically two ways of solving this generalized paradox, which is sometimes called the Super St. Petersburg paradox:
Recently, expected utility theory has been extended to arrive at more behavioral decision models
. In some of these new theories, as in cumulative prospect theory
, the St. Petersburg paradox again appears in certain cases, even when the utility function is concave, but not if it is bounded .
by Daniel Kahneman
and Amos Tversky
. However, their experiments indicated that, very much to the contrary, people tend to overweight small probability events. Therefore the proposed solution by Nicolas Bernoulli is nowadays not considered to be satisfactory.
and John Maynard Keynes
, have rejected maximization of expectation (even of utility) as a proper rule of conduct. Keynes, in particular, insisted that the relative risk of an alternative could be sufficiently high to reject it even were its expectation enormous.
describes the argument:
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, the St. Petersburg paradox is a paradox
Paradox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
related to probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and decision theory
Decision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
. It is based on a particular (theoretical) lottery game (sometimes called St. Petersburg Lottery) that leads to a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
with infinite expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
, i.e., infinite expected payoff, but would nevertheless be considered to be worth only a very small amount of money. The St. Petersburg paradox is a classical situation where a naïve decision criterion (which takes only the expected value into account) would recommend a course of action that no (real) rational
Rationality
In philosophy, rationality is the exercise of reason. It is the manner in which people derive conclusions when considering things deliberately. It also refers to the conformity of one's beliefs with one's reasons for belief, or with one's actions with one's reasons for action...
person would be willing to take. The paradox can be resolved when the decision model is refined via the notion of marginal utility
Marginal utility
In economics, the marginal utility of a good or service is the utility gained from an increase in the consumption of that good or service...
(and it is one origin of notions of utility
Utility
In economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....
functions and of marginal utility), by taking into account the finite resources of the participants, or by noting that one simply cannot buy that which is not sold (and that sellers would not produce a lottery whose expected loss to them were unacceptable).
The paradox is named from Daniel Bernoulli
Daniel Bernoulli
Daniel Bernoulli was a Dutch-Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family. He is particularly remembered for his applications of mathematics to mechanics, especially fluid mechanics, and for his pioneering work in probability and statistics...
's presentation of the problem and his solution, published in 1738 in the Commentaries of the Imperial Academy of Science of Saint Petersburg
Saint Petersburg
Saint Petersburg is a city and a federal subject of Russia located on the Neva River at the head of the Gulf of Finland on the Baltic Sea...
. However, the problem was invented by Daniel's cousin Nicolas Bernoulli
Nicolaus I Bernoulli
Nicolaus Bernoulli , was a Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family....
who first stated it in a letter to Pierre Raymond de Montmort
Pierre Raymond de Montmort
Pierre Rémond de Montmort, a French mathematician, was born in Paris on 27 October 1678, and died there on 7 October 1719. His name was originally just Pierre Rémond or Raymond...
of 9 September 1713 .
The paradox
Consider the following game of chanceGame of chance
A game of chance is a game whose outcome is strongly influenced by some randomizing device, and upon which contestants may or may not wager money or anything of monetary value...
: you pay a fixed fee to enter and then a fair coin is tossed
Coin flipping
Coin flipping or coin tossing or heads or tails is the practice of throwing a coin in the air to choose between two alternatives, sometimes to resolve a dispute between two parties...
repeatedly until a tail appears, ending the game. The pot starts at 1 dollar and is doubled every time a head appears. You win whatever is in the pot after the game ends. Thus you win 1 dollar if a tail appears on the first toss, 2 dollars if a head appears on the first toss and a tail on the second, 4 dollars if a head appears on the first two tosses and a tail on the third, 8 dollars if a head appears on the first three tosses and a tail on the fourth, etc. In short, you win 2k−1 dollars if the coin is tossed k times until the first tail appears.
What would be a fair price to pay for entering the game? To answer this we need to consider what would be the average payout: With probability 1/2, you win 1 dollar; with probability 1/4 you win 2 dollars; with probability 1/8 you win 4 dollars etc. The expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
is thus

This sum diverges to infinity, and so the expected win for the player of this game, at least in its idealized form, in which the casino has unlimited resources, is an infinite amount of money. This means that the player should almost surely
Almost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
come out ahead in the long run, no matter how much he pays to enter; while a large payoff comes along very rarely, when it eventually does it will typically be far more than the amount of money that he has already paid to play. According to the usual treatment of deciding when it is advantageous and therefore rational to play, one should therefore play the game at any price if offered the opportunity. Yet, in published descriptions of the paradox, e.g., , many people expressed disbelief in the result.
Martin quotes Ian Hacking
Ian Hacking
Ian Hacking, CC, FRSC, FBA is a Canadian philosopher, specializing in the philosophy of science.- Life and works :...
as saying "few of us would pay even $25 to enter such a game" and says most commentators would agree.
Expected utility theory
The classical resolution of the paradox involved the explicit introduction of a utility functionUtility
In economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....
, an expected utility hypothesis
Expected utility hypothesis
In economics, game theory, and decision theory the expected utility hypothesis is a theory of utility in which "betting preferences" of people with regard to uncertain outcomes are represented by a function of the payouts , the probabilities of occurrence, risk aversion, and the different utility...
, and the presumption of diminishing marginal utility of money.
In Daniel Bernoulli's own words:
- The determination of the value of an item must not be based on the price, but rather on the utility it yields…. There is no doubt that a gain of one thousand ducatDucatThe ducat is a gold coin that was used as a trade coin throughout Europe before World War I. Its weight is 3.4909 grams of .986 gold, which is 0.1107 troy ounce, actual gold weight...
s is more significant to the pauper than to a rich man though both gain the same amount.
A common utility model, suggested by Bernoulli himself, is the logarithmic function
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
u(w) = ln(w) (known as “log utility”). It is a function of the gambler’s total wealth w, and the concept of diminishing marginal utility of money is built into it. By the expected utility hypothesis, expected utilities can be calculated the same way expected values are. For each possible event, the change in utility ln(wealth after the event) - ln(wealth before the event) will be weighted by the probability of that event occurring. Let c be the cost charged to enter the game. The expected utility of the lottery now converges to a finite value:

This formula gives an implicit relationship between the gambler's wealth and how much he should be willing to pay to play (specifically, any c that gives a positive expected utility). For example, with log utility a millionaire should be willing to pay up to $10.94, a person with $1000 should pay up to $5.94, a person with $2 should pay up to $2, and a person with $0.60 should borrow $0.87 and pay up to $1.47.
Before Daniel Bernoulli published, in 1728, another Swiss mathematician, Gabriel Cramer
Gabriel Cramer
Gabriel Cramer was a Swiss mathematician, born in Geneva. He showed promise in mathematics from an early age. At 18 he received his doctorate and at 20 he was co-chair of mathematics.In 1728 he proposed a solution to the St...
, had already found parts of this idea (also motivated by the St. Petersburg Paradox) in stating that
- the mathematicians estimate money in proportion to its quantity, and men of good sense in proportion to the usage that they may make of it.
He demonstrated in a letter to Nicolas Bernoulli http://www.cs.xu.edu/math/Sources/Montmort/stpetersburg.pdf#search=%22Nicolas%20Bernoulli%22 that a square root function describing the diminishing marginal benefit of gains can resolve the problem. However, unlike Daniel Bernoulli, he did not consider the total wealth of a person, but only the gain by the lottery.
This solution by Cramer and Bernoulli, however, is not yet completely satisfying, since the lottery can easily be changed in a way such that the paradox reappears: To this aim, we just need to change the game so that it gives the (even larger) payoff
 . Again, the game should be worth an infinite amount. More generally, one can find a lottery that allows for a variant of the St. Petersburg paradox for every unbounded utility function, as was first pointed out by .
. Again, the game should be worth an infinite amount. More generally, one can find a lottery that allows for a variant of the St. Petersburg paradox for every unbounded utility function, as was first pointed out by .There are basically two ways of solving this generalized paradox, which is sometimes called the Super St. Petersburg paradox:
- We can take into account that a casino would only offer lotteries with a finite expected value. Under this restriction, it has been proved that the St. Petersburg paradox disappears as long as the utility function is concaveConcave functionIn mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.-Definition:...
, which translates into the assumption that people are (at least for high stakes) risk averseRisk aversionRisk aversion is a concept in psychology, economics, and finance, based on the behavior of humans while exposed to uncertainty....
[Compare ].
- We can assume that the utility function has an upper boundUpper boundIn mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
. Cramer had, in fact, also suggested a simple bounding under which all sums of money beyond some point would have equal utility (id est that the marginal utilityMarginal utilityIn economics, the marginal utility of a good or service is the utility gained from an increase in the consumption of that good or service...
of money would go to zero) , but a utility function need not become constant beyond some point to be bounded; for example the function is bounded above by 1, yet strictly increasing.
is bounded above by 1, yet strictly increasing.
Recently, expected utility theory has been extended to arrive at more behavioral decision models
Behavioral finance
Behavioral economics and its related area of study, behavioral finance, use social, cognitive and emotional factors in understanding the economic decisions of individuals and institutions performing economic functions, including consumers, borrowers and investors, and their effects on market...
. In some of these new theories, as in cumulative prospect theory
Cumulative prospect theory
Cumulative prospect theory is a model for descriptive decisions under risk which was introduced by Amos Tversky and Daniel Kahneman in 1992 . It is a further development and variant of prospect theory...
, the St. Petersburg paradox again appears in certain cases, even when the utility function is concave, but not if it is bounded .
Probability weighting
Nicolas Bernoulli himself proposed an alternative idea for solving the paradox. He conjectured that people will neglect unlikely events . Since in the St. Petersburg lottery only unlikely events yield the high prizes that lead to an infinite expected value, this could resolve the paradox. The idea of probability weighting resurfaced much later in the work on prospect theoryProspect theory
Prospect theory is a theory that describes decisions between alternatives that involve risk i.e. where the probabilities of outcomes are known. The model is descriptive: it tries to model real-life choices, rather than optimal decisions.-Model:...
by Daniel Kahneman
Daniel Kahneman
Daniel Kahneman is an Israeli-American psychologist and Nobel laureate. He is notable for his work on the psychology of judgment and decision-making, behavioral economics and hedonic psychology....
and Amos Tversky
Amos Tversky
Amos Nathan Tversky, was a cognitive and mathematical psychologist, a pioneer of cognitive science, a longtime collaborator of Daniel Kahneman, and a key figure in the discovery of systematic human cognitive bias and handling of risk. Much of his early work concerned the foundations of measurement...
. However, their experiments indicated that, very much to the contrary, people tend to overweight small probability events. Therefore the proposed solution by Nicolas Bernoulli is nowadays not considered to be satisfactory.
Rejection of mathematical expectation
Various authors, including Jean le Rond d'AlembertJean le Rond d'Alembert
Jean-Baptiste le Rond d'Alembert was a French mathematician, mechanician, physicist, philosopher, and music theorist. He was also co-editor with Denis Diderot of the Encyclopédie...
and John Maynard Keynes
John Maynard Keynes
John Maynard Keynes, Baron Keynes of Tilton, CB FBA , was a British economist whose ideas have profoundly affected the theory and practice of modern macroeconomics, as well as the economic policies of governments...
, have rejected maximization of expectation (even of utility) as a proper rule of conduct. Keynes, in particular, insisted that the relative risk of an alternative could be sufficiently high to reject it even were its expectation enormous.
One cannot buy what is not sold
Some economists resolve the paradox by arguing that, even if an entity had infinite resources, the game would never be offered. If the lottery represents an infinite expected gain to the player, then it also represents an infinite expected loss to the host. No one could be observed paying to play the game because it would never be offered. As Paul SamuelsonPaul Samuelson
Paul Anthony Samuelson was an American economist, and the first American to win the Nobel Memorial Prize in Economic Sciences. The Swedish Royal Academies stated, when awarding the prize, that he "has done more than any other contemporary economist to raise the level of scientific analysis in...
describes the argument:
- Paul will never be willing to give as much as Peter will demand for such a contract; and hence the indicated activity will take place at the equilibrium level of zero intensity.
Finite St. Petersburg lotteries
The classical St. Petersburg lottery assumes that the casino has infinite resources. This assumption is often criticized as unrealistic, particularly in connection with the paradox, which involves the reactions of ordinary people to the lottery. Of course, the resources of an actual casino (or any other potential backer of the lottery) are finite. More importantly, the expected value of the lottery only grows logarithmically with the resources of the casino. As a result, the expected value of the lottery, even when played against a casino with the largest resources realistically conceivable, is quite modest. If the total resources (or total maximum jackpot) of the casino are W dollars, then L = 1 + floor(log2(W)) is the maximum number of times the casino can play before it no longer covers the next bet. The expected value E of the lottery then becomes:-

The following table shows the expected value E of the game with various potential bankers and their bankroll W (with the assumption that if you win more than the bankroll you will be paid what the bank has):
Banker Bankroll Expected value of lottery Friendly game $100 $4.28 Millionaire MillionaireA millionaire is an individual whose net worth or wealth is equal to or exceeds one million units of currency. It can also be a person who owns one million units of currency in a bank account or savings account...
$1,000,000 $10.95 Billionaire BillionaireA billionaire, in countries that use the short scale number naming system, is a person who has a net worth of at least one billion units of a given currency, usually the United States dollar, Euro, or Pound sterling. Forbes magazine updates a complete list of U.S. dollar billionaires around the...
$1,000,000,000 $15.93 Bill Gates Bill GatesWilliam Henry "Bill" Gates III is an American business magnate, investor, philanthropist, and author. Gates is the former CEO and current chairman of Microsoft, the software company he founded with Paul Allen...
(2008)$58,000,000,000 $18.84 U.S. GDP (2007) $13.8 trillion $22.79 World GDP (2007) $54.3 trillion $23.77 Googolaire $10100 $166.50
Notes:
The estimated net worth of Bill Gates is from ForbesForbesForbes is an American publishing and media company. Its flagship publication, the Forbes magazine, is published biweekly. Its primary competitors in the national business magazine category are Fortune, which is also published biweekly, and Business Week...
. The GDP data are as estimated for 2007 by the International Monetary FundInternational Monetary FundThe International Monetary Fund is an organization of 187 countries, working to foster global monetary cooperation, secure financial stability, facilitate international trade, promote high employment and sustainable economic growth, and reduce poverty around the world...
, where one trillion dollars equals $1012 (one million times one million dollars). A “googolaire” is a hypothetical person worth a googolGoogolA googol is the large number 10100, that is, the digit 1 followed by 100 zeros:The term was coined in 1938 by 9-year-old Milton Sirotta , nephew of American mathematician Edward Kasner...
dollars ($10100).
A rational person might not find the lottery worth even the modest amounts in the above table, suggesting that the naive decision model of the expected return causes essentially the same problems as for the infinite lottery. Even so, the possible discrepancy between theory and reality is far less dramatic.
The assumption of infinite resources can produce other apparent paradoxes in economics. See martingale (roulette system) and gambler's ruinGambler's ruinThe term gambler's ruin is used for a number of related statistical ideas:* The original meaning is that a gambler who raises his bet to a fixed fraction of bankroll when he wins, but does not reduce it when he loses, will eventually go broke, even if he has a positive expected value on each bet.*...
.
Iterated St. Petersburg lottery
Players may assign a higher value to the game when the lottery is repeatedly played. This can be seen by simulating a typical series of lotteries and accumulating the returns; compare the illustration (right).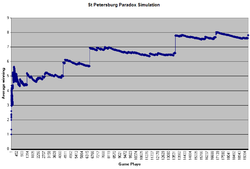
If the expected payout from playing the game once is E1, the expected average per-game payout from playing the game n times is:

Since E1 is infinite, En is infinite as well. Nevertheless, expressing En in this way shows that n, the number of times the game is played, makes a finite contribution to the average per-game payout. The actual average per-game payout obtained in a series of n games is unlikely to fall short of this finite contribution by a significant amount.
To see where the (1/2) log2 n contribution comes from, consider the case of n = 1,024. On average:
- 512 games will pay $1
- 256 games will pay $2
- 128 games will pay $4
- 64 games will pay $8
- 32 games will pay $16
- 16 games will pay $32
- 8 games will pay $64
- 4 games will pay $128
- 2 games will pay $256
- 1 game will pay $512
→ From here on it is equivalent to: 1 game will pay out 1,024 x E1- (1/2) game will pay $1,024
- (1/4) game will pay $2,048
- etc.
The collective average payout is therefore $5,120 (Until the arrow sign) + 1,024 x E1, and the per-game average payout is:

Because the finite contribution from n games is proportional to log2 n, doubling the number of games played leads to a $0.50 increase in the finite contribution. For example, if 2,048 games are played, the finite contribution is $5.50 rather than $5.
It follows that, in order to be reasonably confident of achieving target average per-game winnings of approximately W (where W > $1), we should play approximately 4W games. This will yield a finite contribution equal to W. Unfortunately, the number of games required to be confident of meeting even modest targets is astronomically high. $7 requires approximately 16,000 games, $10 requires approximately 1 million games, and $20 requires approximately 1 trillion games.
Further discussions
The St. Petersburg paradox and the theory of marginal utility have been highly disputed in the past. For a discussion from the point of view of a philosopher, see .
See also
- Exponential growthExponential growthExponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
- Gambler's ruinGambler's ruinThe term gambler's ruin is used for a number of related statistical ideas:* The original meaning is that a gambler who raises his bet to a fixed fraction of bankroll when he wins, but does not reduce it when he loses, will eventually go broke, even if he has a positive expected value on each bet.*...
- Martingale (betting system)Martingale (betting system)Originally, martingale referred to a class of betting strategies popular in 18th century France. The simplest of these strategies was designed for a game in which the gambler wins his stake if a coin comes up heads and loses it if the coin comes up tails...
- Ellsberg paradoxEllsberg paradoxThe Ellsberg paradox is a paradox in decision theory and experimental economics in which people's choices violate the expected utility hypothesis.An alternate viewpoint is that expected utility theory does not properly describe actual human choices...
Works cited
|trans_title= Essays on the analysis of games of chance
|edition= Second
|year= 1713
|publisher= American Mathematical SocietyAmerican Mathematical SocietyThe American Mathematical Society is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, which it does with various publications and conferences as well as annual monetary awards and prizes to mathematicians.The society is one of the...
|type = Reprinted in 2006
|location= Providence, Rhode IslandProvidence, Rhode IslandProvidence is the capital and most populous city of Rhode Island and was one of the first cities established in the United States. Located in Providence County, it is the third largest city in the New England region...
|language=
|isbn= 978-0821837818
| ref = harv
}} as translated and posted at
(Publicly accessible, older version.)
External links



