
Stable manifold theorem
Encyclopedia
In mathematics
, especially in the study of dynamical system
s and differential equation
s, the stable manifold theorem is an important result about the structure of the set of orbits
approaching a given hyperbolic fixed point.
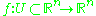
be a smooth map with hyperbolic fixed point at p. We denote by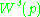 the stable set
the stable set
and by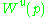 the unstable set of p.
the unstable set of p.
The theorem states that
Accordingly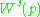 is a stable manifold
is a stable manifold
and is an unstable manifold.
is an unstable manifold.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the study of dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s and differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s, the stable manifold theorem is an important result about the structure of the set of orbits
Orbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
approaching a given hyperbolic fixed point.
Stable manifold theorem
Let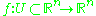
be a smooth map with hyperbolic fixed point at p. We denote by
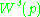 the stable set
the stable setStable set
The term stable set may refer to:* The independent set in graph theory, the set of vertices of a graph not directly connected by edges.* The stable set in dynamical systems, the set of points leading up to an attractor....
and by
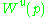 the unstable set of p.
the unstable set of p.The theorem states that
-
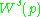 is a smooth manifold and its tangent spaceTangent spaceIn mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
is a smooth manifold and its tangent spaceTangent spaceIn mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
has the same dimension as the stable space of the linearizationLinearizationIn mathematics and its applications, linearization refers to finding the linear approximation to a function at a given point. In the study of dynamical systems, linearization is a method for assessing the local stability of an equilibrium point of a system of nonlinear differential equations or...
of f at p. -
 is a smooth manifold and its tangent space has the same dimension as the unstable space of the linearization of f at p.
is a smooth manifold and its tangent space has the same dimension as the unstable space of the linearization of f at p.
Accordingly
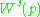 is a stable manifold
is a stable manifoldStable manifold
In mathematics, and in particular the study of dynamical systems, the idea of stable and unstable sets or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor or repellor...
and
 is an unstable manifold.
is an unstable manifold.

