Stellar structure
Encyclopedia
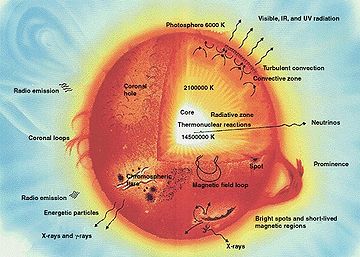
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
s of different mass and age have varying internal structures. Stellar structure models describe the internal structure of a star in detail and make detailed predictions about the luminosity
Luminosity
Luminosity is a measurement of brightness.-In photometry and color imaging:In photometry, luminosity is sometimes incorrectly used to refer to luminance, which is the density of luminous intensity in a given direction. The SI unit for luminance is candela per square metre.The luminosity function...
, the color
Stellar classification
In astronomy, stellar classification is a classification of stars based on their spectral characteristics. The spectral class of a star is a designated class of a star describing the ionization of its chromosphere, what atomic excitations are most prominent in the light, giving an objective measure...
and the future evolution
Stellar evolution
Stellar evolution is the process by which a star undergoes a sequence of radical changes during its lifetime. Depending on the mass of the star, this lifetime ranges from only a few million years to trillions of years .Stellar evolution is not studied by observing the life of a single...
of the star.
Energy transport
Convection
Convection is the movement of molecules within fluids and rheids. It cannot take place in solids, since neither bulk current flows nor significant diffusion can take place in solids....
and radiative transfer
Radiative transfer
Radiative transfer is the physical phenomenon of energy transfer in the form of electromagnetic radiation. The propagation of radiation through a medium is affected by absorption, emission and scattering processes. The equation of radiative transfer describes these interactions mathematically...
, but thermal conduction
Heat conduction
In heat transfer, conduction is a mode of transfer of energy within and between bodies of matter, due to a temperature gradient. Conduction means collisional and diffusive transfer of kinetic energy of particles of ponderable matter . Conduction takes place in all forms of ponderable matter, viz....
is important in white dwarf
White dwarf
A white dwarf, also called a degenerate dwarf, is a small star composed mostly of electron-degenerate matter. They are very dense; a white dwarf's mass is comparable to that of the Sun and its volume is comparable to that of the Earth. Its faint luminosity comes from the emission of stored...
s.
Convection is the dominant mode of energy transport when the temperature gradient is steep enough so that a given parcel of gas within the star will continue to rise if it rises slightly via an adiabatic process
Adiabatic process
In thermodynamics, an adiabatic process or an isocaloric process is a thermodynamic process in which the net heat transfer to or from the working fluid is zero. Such a process can occur if the container of the system has thermally-insulated walls or the process happens in an extremely short time,...
. In this case, the rising parcel is buoyant and continues to rise if it is warmer than the surrounding gas; if the rising particle is cooler than the surrounding gas, it will fall back to its original height. In regions with a low temperature gradient and a low enough opacity
Opacity (optics)
Opacity is the measure of impenetrability to electromagnetic or other kinds of radiation, especially visible light. In radiative transfer, it describes the absorption and scattering of radiation in a medium, such as a plasma, dielectric, shielding material, glass, etc...
to allow energy transport via radiation, radiation is the dominant mode of energy transport.
The internal structure of a main sequence
Main sequence
The main sequence is a continuous and distinctive band of stars that appears on plots of stellar color versus brightness. These color-magnitude plots are known as Hertzsprung–Russell diagrams after their co-developers, Ejnar Hertzsprung and Henry Norris Russell...
star depends upon the mass of the star.
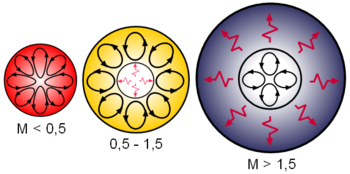
In solar mass stars (0.3–1.5 solar mass
Solar mass
The solar mass , , is a standard unit of mass in astronomy, used to indicate the masses of other stars and galaxies...
es), including the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
, hydrogen-to-helium fusion occurs primarily via proton-proton chains, which do not establish a steep temperature gradient. Thus, radiation dominates in the inner portion of solar mass stars. The outer portion of solar mass stars is cool enough that hydrogen is neutral and thus opaque to ultraviolet photons, so convection dominates. Therefore, solar mass stars have radiative cores with convective envelopes in the outer portion of the star.
In massive stars (greater than about 1.5 solar mass
Solar mass
The solar mass , , is a standard unit of mass in astronomy, used to indicate the masses of other stars and galaxies...
es), the core temperature is above about 1.8×107 K
Kelvin
The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
, so hydrogen
Hydrogen
Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly...
-to-helium
Helium
Helium is the chemical element with atomic number 2 and an atomic weight of 4.002602, which is represented by the symbol He. It is a colorless, odorless, tasteless, non-toxic, inert, monatomic gas that heads the noble gas group in the periodic table...
fusion
Nuclear fusion
Nuclear fusion is the process by which two or more atomic nuclei join together, or "fuse", to form a single heavier nucleus. This is usually accompanied by the release or absorption of large quantities of energy...
occurs primarily via the CNO cycle
CNO cycle
The CNO cycle is one of two sets of fusion reactions by which stars convert hydrogen to helium, the other being the proton–proton chain. Unlike the proton–proton chain reaction, the CNO cycle is a catalytic cycle. Theoretical models show that the CNO cycle is the dominant source of energy in stars...
. In the CNO cycle, the energy generation rate scales as the temperature to the 17th power, whereas the rate scales as the temperature to the 4th power in the proton-proton chains. Due to the strong temperature sensitivity of the CNO cycle, the temperature gradient in the inner portion of the star is steep enough to make the core convective
Convection zone
The convection zone of a star is the range of radii in which energy is transported primarily by convection. In the radiation zone, energy is transported by radiation...
. In the outer portion of the star, the temperature gradient is shallower but the temperature is high enough that the hydrogen is nearly fully ionized, so the star remains transparent to ultraviolet radiation. Thus, massive stars have a radiative
Radiation zone
The radiation zone is the middle zone in the Sun's interior. Energy travels out of the core into the radiation zone. Energy that travels through the radiation zone is in the form of electromagnetic radiation. The radiation zone is so dense that the waves bounce around...
envelope.
The lowest mass main sequence stars have no radiation zone; the dominant energy transport mechanism throughout the star is convection. Giants
Giant star
A giant star is a star with substantially larger radius and luminosity than a main sequence star of the same surface temperature. Typically, giant stars have radii between 10 and 100 solar radii and luminosities between 10 and 1,000 times that of the Sun. Stars still more luminous than giants are...
are also fully convective.
Equations of stellar structure
The simplest commonly used model of stellar structure is the spherically symmetric quasi-static model, which assumes that a starStar
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
is in a steady state
Steady state
A system in a steady state has numerous properties that are unchanging in time. This implies that for any property p of the system, the partial derivative with respect to time is zero:...
and that it is spherically symmetric
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
. It contains four basic first-order differential equations: two represent how matter
Matter
Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...
and pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
vary with radius; two represent how temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
and luminosity
Luminosity
Luminosity is a measurement of brightness.-In photometry and color imaging:In photometry, luminosity is sometimes incorrectly used to refer to luminance, which is the density of luminous intensity in a given direction. The SI unit for luminance is candela per square metre.The luminosity function...
vary with radius.
In forming the stellar structure equations (exploiting the assumed spherical symmetry), one considers the matter density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
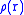, temperatureTemperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
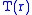, total pressurePressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
(matter plus radiation)
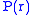, luminosityLuminosity
Luminosity is a measurement of brightness.-In photometry and color imaging:In photometry, luminosity is sometimes incorrectly used to refer to luminance, which is the density of luminous intensity in a given direction. The SI unit for luminance is candela per square metre.The luminosity function...
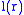, and energy generation rate per unit mass 
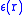in a spherical shell of a thickness 
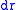at a distance 
from the center of the star. The star is assumed to be in local thermodynamic equilibrium (LTE) so the temperature is identical for matterMatter
Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...
and photons. Although LTE does not strictly hold because the temperature a given shell "sees" below itself is always hotter than the temperature above, this approximation is normally excellent because the photon mean free path
Mean free path
In physics, the mean free path is the average distance covered by a moving particle between successive impacts which modify its direction or energy or other particle properties.-Derivation:...
,
, is much smaller than the length over which the temperature varies considerably, i. e.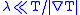 
.First is a statement of hydrostatic equilibrium
Hydrostatic equilibrium
Hydrostatic equilibrium or hydrostatic balance is the condition in fluid mechanics where a volume of a fluid is at rest or at constant velocity. This occurs when compression due to gravity is balanced by a pressure gradient force...
: the outward force due to the pressure gradient
Pressure gradient
In atmospheric sciences , the pressure gradient is a physical quantity that describes in which direction and at what rate the pressure changes the most rapidly around a particular location. The pressure gradient is a dimensional quantity expressed in units of pressure per unit length...
within the star is exactly balanced by the inward force due to gravity.
,where
is the cumulative mass inside the shell at 
and G is the gravitational constantGravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
. The cumulative mass increases with radius according to the mass continuity equation
Continuity equation
A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
:
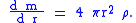
Integrating
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
the mass continuity equation from the star center (
) to the radius of the star (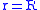
) yields the total mass of the star.Considering the energy leaving the spherical shell yields the energy equation:
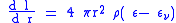,where
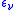is the luminosity produced in the form of neutrinos (which usually escape the star without interacting with ordinary matter) per unit mass. Outside the core of the star, where nuclear reactions occur, no energy is generated, so the luminosity is constant.The energy transport equation takes differing forms depending upon the mode of energy transport. For conductive luminosity transport (appropriate for a white dwarf
White dwarf
A white dwarf, also called a degenerate dwarf, is a small star composed mostly of electron-degenerate matter. They are very dense; a white dwarf's mass is comparable to that of the Sun and its volume is comparable to that of the Earth. Its faint luminosity comes from the emission of stored...
), the energy equation is
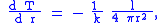
where k is the thermal conductivity
Thermal conductivity
In physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
.
In the case of radiative energy transport, appropriate for the inner portion of a solar mass main sequence
Main sequence
The main sequence is a continuous and distinctive band of stars that appears on plots of stellar color versus brightness. These color-magnitude plots are known as Hertzsprung–Russell diagrams after their co-developers, Ejnar Hertzsprung and Henry Norris Russell...
star and the outer envelope of a massive main sequence star,
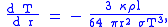
where
is the opacityOpacity (optics)
Opacity is the measure of impenetrability to electromagnetic or other kinds of radiation, especially visible light. In radiative transfer, it describes the absorption and scattering of radiation in a medium, such as a plasma, dielectric, shielding material, glass, etc...
of the matter,
is the Stefan-Boltzmann constantStefan-Boltzmann constant
The Stefan–Boltzmann constant , a physical constant denoted by the Greek letter σ, is the constant of proportionality in the Stefan–Boltzmann law: the total energy radiated per unit surface area of a black body in unit time is proportional to the fourth power of the thermodynamic temperature.The...
, and the Boltzmann constant is set to one.
The case of convective luminosity transport (appropriate for non-radiative portions of main sequence stars and all of giants and low mass stars) does not have a known rigorous mathematical formulation, and involves turbulence
Turbulence
In fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic and stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time...
in the gas. Convective energy transport is usually modeled using mixing length theory
Mixing length theory
In fluid dynamics, mixing length model is a method attempting to describe momentum transfer by turbulence Reynolds stresses within a newtonian fluid boundary layer by means of an eddy viscosity. The model was developed by Ludwig Prandtl in the early 20th century...
. This treats the gas in the star as containing discrete elements which roughly retain the temperature, density, and pressure of their surroundings but move through the star as far as a characteristic length, called the mixing length. For a monatomic ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
, when the convection is adiabatic, meaning that the convective gas bubbles don't exchange heat with their surroundings, mixing length theory yields
where
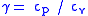is the adiabatic index, the ratio of specific heats in the gas. (For a fully ionized ideal gasIdeal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
,
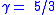.) When the convection is not adiabatic, the true temperature gradient is not given by this equation. For example, in the Sun the convection at the base of the convection zone, near the core, is adiabatic but that near the surface is not. The mixing length theory contains two free parameters which must be set to make the model fit observations, so it is a phenomelogical theory rather than a rigorous mathematical formulation.Also required are the equations of state
Equation of state
In physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...
, relating the pressure, opacity and energy generation rate to other local variables appropriate for the material, such as temperature, density, chemical composition, etc. Relevant equations of state for pressure may have to include the perfect gas law, radiation pressure, pressure due to degenerate electrons, etc. Opacity cannot be expressed exactly by a single formula. It is calculated for various compositions at specific densities and temperatures and presented in tabular form. Stellar structure codes (meaning computer programs calculating the model's variables) either interpolate in a density-temperature grid to obtain the opacity needed, or use a fitting function
Curve fitting
Curve fitting is the process of constructing a curve, or mathematical function, that has the best fit to a series of data points, possibly subject to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is required, or smoothing, in which a "smooth" function...
based on the tabulated values. A similar situation occurs for accurate calculations of the pressure equation of state. Finally, the nuclear energy generation rate is computed from particle physics experiments, using reaction networks to compute reaction rates for each individual reaction step and equilibrium abundances for each isotope in the gas.
Combined with a set of boundary conditions, a solution of these equations completely describes the behavior of the star. Typical boundary conditions set the values of the observable parameters appropriately at the surface (
) and center (
) of the star: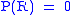 
, meaning the pressure at the surface of the star is zero; 
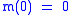, there is no mass inside the center of the star, as required if the mass density remains finite; 
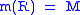, the total mass of the star is the star's mass; and 
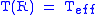, the temperature at the surface is the effective temperatureEffective temperature
The effective temperature of a body such as a star or planet is the temperature of a black body that would emit the same total amount of electromagnetic radiation...
of the star.
Although nowadays stellar evolution models describes the main features of color magnitude diagrams, important improvements have to be made in order to remove uncertainties which are linked to the limited knowledge of transport phenomena. The most difficult challenge remains the numerical treatment of turbulence. Some research teams are developing simplified modelling of turbulence in 3D calculations.
Rapid evolution
The above simplified model is not adequate without modification in situations when the composition changes are sufficiently rapid. The equation of hydrostatic equilibrium may need to be modified by adding a radial acceleration term if the radius of the star is changing very quickly, for example if the star is radially pulsating. Also, if the nuclear burning is not stable, or the star's core is rapidly collapsing, an entropy term must be added to the energy equation.External links
- OPAL opacity code retrieved November 2009
- The Yellow CESAM code, stellar evolution and structure FORTRANFortranFortran is a general-purpose, procedural, imperative programming language that is especially suited to numeric computation and scientific computing...
source code - EZ to Evolve ZAMS Stars a FORTRAN 90 software derived from Eggleton's Stellar Evolution Code, a web-based interface can be found here http://shayol.bartol.udel.edu/~rhdt/ezweb.
- Geneva Grids of Stellar Evolution Models (some of them including rotational induced mixing)
- The BaSTI database of stellar evolution tracks