Stochastic equicontinuity
Encyclopedia
In estimation theory
in statistics
, stochastic equicontinuity is a property of estimator
s or of estimation procedures that is useful in dealing with their asymptotic behviour
as the amount of data increases. It is a version of equicontinuity
used in the context of functions of random variables: that is, random function
s. The property relates to the rate of convergence
of sequences of random variables and requires that this rate is essentially the same within a region of the parameter space
being considered.
For instance, stochastic equicontinuity, along with other conditions, can be used to show uniform weak convergence, which can be used to prove the convergence
of extremum estimator
s.
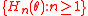be a family of random functions defined from 
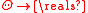, where 
is any normed metric space. Here 
might represent a sequence of estimators applied to datasets of size n, given that the data arises from a population for which the parameter indexing the statistical model for the data is θ. The randomness of the functions arises from the data generating process
under which a set of observed data is considered to be a realisation of a probabilistic or statistical model. However, in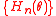
, θ relates to the model currently being postulated or fitted rather than to an underlying model which is supposed to represent the mechanism generating the data. Then 
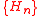is stochastically equicontinuous if, for every 
, there is a 
such that:
Here B(θ, δ) represents a ball in the parameter space, centred at θ and whose radius depends on δ.
Estimation theory
Estimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
in statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, stochastic equicontinuity is a property of estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
s or of estimation procedures that is useful in dealing with their asymptotic behviour
Asymptotic theory (statistics)
In statistics, asymptotic theory, or large sample theory, is a generic framework for assessment of properties of estimators and statistical tests...
as the amount of data increases. It is a version of equicontinuity
Equicontinuity
In mathematical analysis, a family of functions is equicontinuous if all the functions are continuous and they have equal variation over a given neighbourhood, in a precise sense described herein...
used in the context of functions of random variables: that is, random function
Random function
A random function is a function chosen at random from a finite family of functions. Typically, the family consists of the set of all maps from the domain to the codomain. Thus, a random function can be considered to map each input independently at random to any one of the possible outputs. Viewed...
s. The property relates to the rate of convergence
Convergence of random variables
In probability theory, there exist several different notions of convergence of random variables. The convergence of sequences of random variables to some limit random variable is an important concept in probability theory, and its applications to statistics and stochastic processes...
of sequences of random variables and requires that this rate is essentially the same within a region of the parameter space
Parameter space
In science, a parameter space is the set of values of parameters encountered in a particular mathematical model. Often the parameters are inputs of a function, in which case the technical term for the parameter space is domain of a function....
being considered.
For instance, stochastic equicontinuity, along with other conditions, can be used to show uniform weak convergence, which can be used to prove the convergence
Convergence of random variables
In probability theory, there exist several different notions of convergence of random variables. The convergence of sequences of random variables to some limit random variable is an important concept in probability theory, and its applications to statistics and stochastic processes...
of extremum estimator
Extremum estimator
In statistics and econometrics, extremum estimators is a wide class of estimators for parametric models that are calculated through maximization of a certain objective function, which depends on the data...
s.
Definition
Let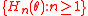 be a family of random functions defined from 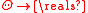, where is any normed metric space. Here might represent a sequence of estimators applied to datasets of size n, given that the data arises from a population for which the parameter indexing the statistical model for the data is θ. The randomness of the functions arises from the data generating processData generating process
The term data generating process is used in statistical and scientific literature to convey a number of different ideas:*the data collection process, being routes and procedures by which data reach a database ;...
under which a set of observed data is considered to be a realisation of a probabilistic or statistical model. However, in
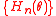, θ relates to the model currently being postulated or fitted rather than to an underlying model which is supposed to represent the mechanism generating the data. Then 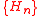is stochastically equicontinuous if, for every , there is a such that:Here B(θ, δ) represents a ball in the parameter space, centred at θ and whose radius depends on δ.