
Strong gravitational lensing
Encyclopedia
Strong gravitational lensing is a gravitational lensing effect that is strong enough to produce multiple images, arcs, or even Einstein ring
s. Generally, the strong lensing effect requires the projected lens mass density greater than the critical density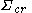 . For point-like background sources, there will be multiple images; for extended background emissions, there can be arcs or rings. Topologically, the multiple image production is governed by Odd number theorem
. For point-like background sources, there will be multiple images; for extended background emissions, there can be arcs or rings. Topologically, the multiple image production is governed by Odd number theorem
.
Einstein ring
In observational astronomy an Einstein ring is the deformation of the light from a source into a ring through gravitational lensing of the source's light by an object with an extremely large mass . This occurs when the source, lens and observer are all aligned...
s. Generally, the strong lensing effect requires the projected lens mass density greater than the critical density
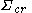 . For point-like background sources, there will be multiple images; for extended background emissions, there can be arcs or rings. Topologically, the multiple image production is governed by Odd number theorem
. For point-like background sources, there will be multiple images; for extended background emissions, there can be arcs or rings. Topologically, the multiple image production is governed by Odd number theoremOdd number theorem
The odd number theorem is a theorem in strong gravitational lensing which comes directly from differential topology. It says that the number of multiple images produced by a bounded transparent lens must be odd....
.

