
Odd number theorem
Encyclopedia
The odd number theorem is a theorem in strong gravitational lensing which comes directly from differential topology
. It says that the number of multiple images produced by a bounded transparent lens must be odd.
In fact, the gravitational lensing is a mapping from image plane to source plane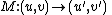 . If we use direction cosines describing the bended light rays, we can write a vector field on
. If we use direction cosines describing the bended light rays, we can write a vector field on 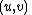 plane
plane 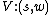 . However, only in some specific directions
. However, only in some specific directions 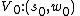 , the bended light rays will reach the observer, i.e., the images only forms where
, the bended light rays will reach the observer, i.e., the images only forms where 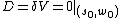 . Then we can directly apply Poincaré–Hopf theorem
. Then we can directly apply Poincaré–Hopf theorem
 . The index of sources and sinks is +1, and that of saddle points is −1. So the Euler characteristic
. The index of sources and sinks is +1, and that of saddle points is −1. So the Euler characteristic
equals the difference between the number of positive indice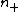 and the number of negative indice
and the number of negative indice 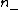 . For the far field case, there is only one image, i.e.,
. For the far field case, there is only one image, i.e., 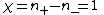 . So the total number of images is
. So the total number of images is 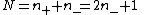 , i.e., odd. The strict proof needs Uhlenbeck’s Morse theory
, i.e., odd. The strict proof needs Uhlenbeck’s Morse theory
of null geodesics.
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
. It says that the number of multiple images produced by a bounded transparent lens must be odd.
In fact, the gravitational lensing is a mapping from image plane to source plane
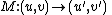 . If we use direction cosines describing the bended light rays, we can write a vector field on
. If we use direction cosines describing the bended light rays, we can write a vector field on 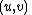 plane
plane 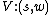 . However, only in some specific directions
. However, only in some specific directions 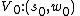 , the bended light rays will reach the observer, i.e., the images only forms where
, the bended light rays will reach the observer, i.e., the images only forms where 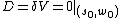 . Then we can directly apply Poincaré–Hopf theorem
. Then we can directly apply Poincaré–Hopf theoremPoincaré–Hopf theorem
In mathematics, the Poincaré–Hopf theorem is an important theorem that is still used today in differential topology...
 . The index of sources and sinks is +1, and that of saddle points is −1. So the Euler characteristic
. The index of sources and sinks is +1, and that of saddle points is −1. So the Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
equals the difference between the number of positive indice
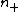 and the number of negative indice
and the number of negative indice 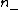 . For the far field case, there is only one image, i.e.,
. For the far field case, there is only one image, i.e., 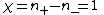 . So the total number of images is
. So the total number of images is 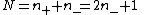 , i.e., odd. The strict proof needs Uhlenbeck’s Morse theory
, i.e., odd. The strict proof needs Uhlenbeck’s Morse theoryMorse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
of null geodesics.

