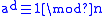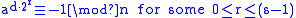Strong pseudoprime
Encyclopedia
In number theory
, a strong pseudoprime is a composite number
that passes a primality test. All primes pass this test, but a small fraction of composites pass as well, making them "false primes
". Unlike the Fermat pseudoprimes, for which there exist numbers that are pseudoprimes to all coprime
bases (the Carmichael numbers), there are no composites that are strong pseudoprimes to all bases.
The definition of a strong pseudoprime depends on the base used; different bases have different strong pseudoprimes. The definition is trivially met if so these base choices are often excluded.
Guy
mistakenly gives a definition with only the first condition, which is not satisfied by all primes.
and a Fermat pseudoprime to that base, but not all Euler and Fermat pseudoprimes are strong pseudoprimes. Carmichael numbers may be strong pseudoprimes to some bases—for example, 561 is a strong pseudoprime to base 50—but not to all bases.
A composite number n is a strong pseudoprime to at most one quarter of all bases below n ; thus, there are no "strong Carmichael numbers", numbers that are strong pseudoprimes to all bases. Thus given a random base, the probability that a number is a strong pseudoprime to that base is less than 1/4, forming the basis of the widely-used Miller-Rabin primality test
. However, there are still infinitely many strong pseudoprimes to any base.
The first to base 3 are
The first to base 5 are
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a strong pseudoprime is a composite number
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
that passes a primality test. All primes pass this test, but a small fraction of composites pass as well, making them "false primes
Pseudoprime
In number theory, the Fermat pseudoprimes make up the most important class of pseudoprimes that come from Fermat's little theorem.- Definition :...
". Unlike the Fermat pseudoprimes, for which there exist numbers that are pseudoprimes to all coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
bases (the Carmichael numbers), there are no composites that are strong pseudoprimes to all bases.
Formal definition
Formally, a composite number n = d · 2s + 1 with d being odd is called a strong pseudoprime to a relatively prime base a when one of the following conditions hold:The definition of a strong pseudoprime depends on the base used; different bases have different strong pseudoprimes. The definition is trivially met if so these base choices are often excluded.
Guy
Richard K. Guy
Richard Kenneth Guy is a British mathematician, Professor Emeritus in the Department of Mathematics at the University of Calgary....
mistakenly gives a definition with only the first condition, which is not satisfied by all primes.
Properties of strong pseudoprimes
A strong pseudoprime to base a is always an Euler pseudoprimeEuler pseudoprime
In arithmetic, an odd composite integer n is called an Euler pseudoprime to base a, if a and n are coprime, and....
and a Fermat pseudoprime to that base, but not all Euler and Fermat pseudoprimes are strong pseudoprimes. Carmichael numbers may be strong pseudoprimes to some bases—for example, 561 is a strong pseudoprime to base 50—but not to all bases.
A composite number n is a strong pseudoprime to at most one quarter of all bases below n ; thus, there are no "strong Carmichael numbers", numbers that are strong pseudoprimes to all bases. Thus given a random base, the probability that a number is a strong pseudoprime to that base is less than 1/4, forming the basis of the widely-used Miller-Rabin primality test
Miller-Rabin primality test
The Miller–Rabin primality test or Rabin–Miller primality test is a primality test: an algorithmwhich determines whether a given number is prime,...
. However, there are still infinitely many strong pseudoprimes to any base.
Examples
The first strong pseudoprimes to base 2 are- 2047, 3277, 4033, 4681, 8321, 15841, 29341, 42799, 49141, 52633, 65281, 74665, 80581, 85489, 88357, 90751, ... .
The first to base 3 are
- 121, 703, 1891, 3281, 8401, 8911, 10585, 12403, 16531, 18721, 19345, 23521, 31621, 44287, 47197, 55969, 63139, 74593, 79003, 82513, 87913, 88573, 97567, ... .
The first to base 5 are
- 781, 1541, 5461, 5611, 7813, 13021, 14981, 15751, 24211, 25351, 29539, 38081, 40501, 44801, 53971, 79381, ... .