Structured SVM
Encyclopedia
The structured support vector machine is a machine learning
algorithm that generalizes the Support Vector Machine
(SVM) classifier. Whereas the SVM classifier supports binary classification
, multiclass classification
and regression
, the structured SVM allows training of a classifier for general structured output labels
.
As an example, a sample instance might be a natural language sentence, and the output label is an annotated parse tree. Training a classifier consists of showing pairs of correct sample and output label pairs. After training, the structured SVM model allows one to predict for new sample instances the corresponding output label; that is, given a natural language sentence, the classifier can produce the most likely parse tree
.
For a set of
training instances 
, 
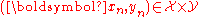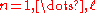from a sample space 
and label space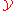 
, the structured SVM minimizes the following regularized risk function.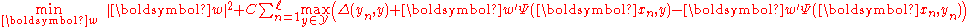
The function is convex in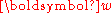
because the maximum of a set of affine functions is convex. The function 
measures a distance in label space and is an arbitrary function (not necessarily a metric
) satisfying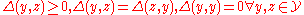
. The function 
is a feature function, extracting some feature vector from a given sample and label. The design of this function depends very much on the application.
Because the regularized risk function above is non-differentiable, it is often reformulated in terms of a quadratic program by introducing one slack variables
for each sample, each representing the value of the maximum. The standard structured SVM primal formulation is given as follows.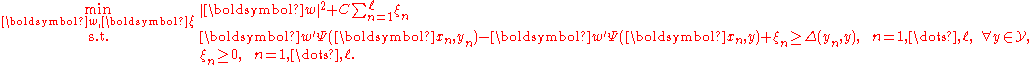
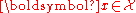is known, and a prediction function 
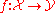maps it to a predicted label from the label space 
. For structured SVMs, given the vector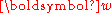 
obtained from training, the prediction function is the following.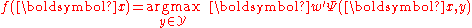
Therefore, the maximizer over the label space is the predicted label. Solving for this maximizer is the so called inference problem and similar to making a maximum a-posteriori (MAP) prediction in probabilistic models. Depending on the structure of the function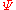
, solving for the maximizer can be a hard problem.
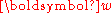violates constraints of the complete set inequalities, a separation
problem needs to be solved. As the inequalities decompose over the samples, for each sample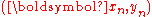
the following problem needs to be solved.
The right hand side objective to be maximized is composed of the constant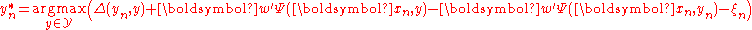
and a term dependent on the variables optimized over, namely 
. If the achieved right hand side objective is smaller or equal to zero, no violated constraint for this sample exist. If it is strictly larger than zero, the most violated constraint with respect to this sample has been identified. The problem is enlarged by this constraint and resolved. The process continues until no violated inequalities can be identified.
If the constants are dropped from the above problem, we obtain the following problem to be solved.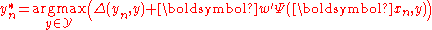
This problem looks very similar to the inference problem. The only difference is the addition of the term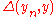
. Most often, it is chosen such that it has a natural decomposition in label space. In that case, the influence of 
can be encoded into the inference problem and solving for the most violating constraint is equivalent to solving the inference problem.
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
algorithm that generalizes the Support Vector Machine
Support vector machine
A support vector machine is a concept in statistics and computer science for a set of related supervised learning methods that analyze data and recognize patterns, used for classification and regression analysis...
(SVM) classifier. Whereas the SVM classifier supports binary classification
Binary classification
Binary classification is the task of classifying the members of a given set of objects into two groups on the basis of whether they have some property or not. Some typical binary classification tasks are...
, multiclass classification
Multiclass classification
In machine learning, multiclass or multinomial classification is the problem of classifying instances into more than two classes.While some classification algorithms naturally permit the use of more than two classes, others are by nature binary algorithms; these can, however, be turned into...
and regression
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
, the structured SVM allows training of a classifier for general structured output labels
Structured learning
Structured learning is the subfield of machine learning concerned with computer programs that learn to map inputs to arbitrarily complex outputs. This stands in contrast to the simpler approaches of classification, where input data are mapped to "atomic" labels, i.e...
.
As an example, a sample instance might be a natural language sentence, and the output label is an annotated parse tree. Training a classifier consists of showing pairs of correct sample and output label pairs. After training, the structured SVM model allows one to predict for new sample instances the corresponding output label; that is, given a natural language sentence, the classifier can produce the most likely parse tree
Parse tree
A concrete syntax tree or parse tree or parsing treeis an ordered, rooted tree that represents the syntactic structure of a string according to some formal grammar. In a parse tree, the interior nodes are labeled by non-terminals of the grammar, while the leaf nodes are labeled by terminals of the...
.
For a set of
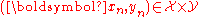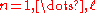training instances , from a sample space and label space 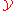, the structured SVM minimizes the following regularized risk function.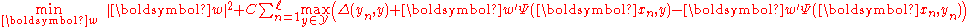The function is convex in
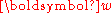because the maximum of a set of affine functions is convex. The function measures a distance in label space and is an arbitrary function (not necessarily a metricMetric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
) satisfying
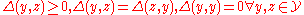. The function is a feature function, extracting some feature vector from a given sample and label. The design of this function depends very much on the application.Because the regularized risk function above is non-differentiable, it is often reformulated in terms of a quadratic program by introducing one slack variables
for each sample, each representing the value of the maximum. The standard structured SVM primal formulation is given as follows.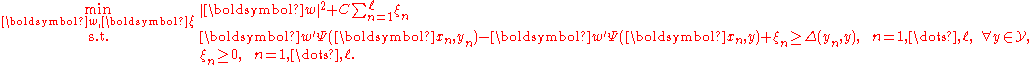Inference problem
At test time, only a sample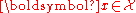 is known, and a prediction function 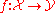maps it to a predicted label from the label space . For structured SVMs, given the vector 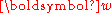obtained from training, the prediction function is the following.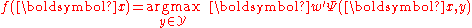Therefore, the maximizer over the label space is the predicted label. Solving for this maximizer is the so called inference problem and similar to making a maximum a-posteriori (MAP) prediction in probabilistic models. Depending on the structure of the function
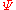, solving for the maximizer can be a hard problem.Separation
The above quadratic program involves a very large, possibly infinite number of linear inequality constraints. In general, the number of inequalities is too large to be optimized over explicitly. Instead the problem is solved by using delayed constraint generation where only a finite and small subset of the constraints is used. Optimizing over a subset of the constraints enlarges the feasible set and will yield a solution which provides a lower bound on the objective. To test whether the solution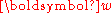 violates constraints of the complete set inequalities, a separationSeparation
Separation may refer to:* Separation , the process by which a service member leaves active duty* Separation , rules to minimise the risk of collision between aircraft in flight...
problem needs to be solved. As the inequalities decompose over the samples, for each sample
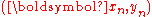the following problem needs to be solved.The right hand side objective to be maximized is composed of the constant
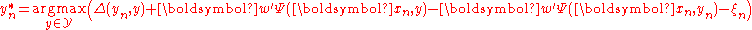and a term dependent on the variables optimized over, namely . If the achieved right hand side objective is smaller or equal to zero, no violated constraint for this sample exist. If it is strictly larger than zero, the most violated constraint with respect to this sample has been identified. The problem is enlarged by this constraint and resolved. The process continues until no violated inequalities can be identified.If the constants are dropped from the above problem, we obtain the following problem to be solved.
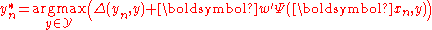
This problem looks very similar to the inference problem. The only difference is the addition of the term
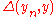. Most often, it is chosen such that it has a natural decomposition in label space. In that case, the influence of can be encoded into the inference problem and solving for the most violating constraint is equivalent to solving the inference problem.