
Sum-free set
Encyclopedia
In additive combinatorics and number theory
, a subset A of an abelian group
G is said to be sum-free if the sumset
A⊕A is disjoint from A. In other words, A is sum-free if the equation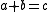 has no solution with
has no solution with 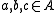 .
.
For example, the set of odd numbers
is a sum-free subset of the integers, and the set {N/2+1, ..., N} forms a large sum-free subset of the set {1,...,N} (N even).
Some basic questions that have been asked about sum-free sets are:
A sum-free set is said to be maximal if it is not a proper subset of another sum-free set.
Additive number theory
In number theory, the specialty additive number theory studies subsets of integers and their behavior under addition. More abstractly, the field of "additive number theory" includes the study of Abelian groups and commutative semigroups with an operation of addition. Additive number theory has...
, a subset A of an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
G is said to be sum-free if the sumset
Sumset
In additive combinatorics, the sumset of two subsets A and B of an abelian group G is defined to be the set of all sums of an element from A with an element from B...
A⊕A is disjoint from A. In other words, A is sum-free if the equation
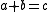 has no solution with
has no solution with 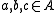 .
.For example, the set of odd numbers
Even and odd numbers
In mathematics, the parity of an object states whether it is even or odd.This concept begins with integers. An even number is an integer that is "evenly divisible" by 2, i.e., divisible by 2 without remainder; an odd number is an integer that is not evenly divisible by 2...
is a sum-free subset of the integers, and the set {N/2+1, ..., N} forms a large sum-free subset of the set {1,...,N} (N even).
Some basic questions that have been asked about sum-free sets are:
- How many sum-free subsets of {1, ..., N} are there, for an integer N? Ben Green has shown that the answer is
 , as predicted by the Cameron–Erdős conjecture (see Sloane's ).
, as predicted by the Cameron–Erdős conjecture (see Sloane's ). - How many sum-free sets does an abelian group G contain?
- What is the size of the largest sum-free set that an abelian group G contains?
A sum-free set is said to be maximal if it is not a proper subset of another sum-free set.

