Symmetric hypergraph theorem
Encyclopedia
The Symmetric hypergraph theorem is a theorem in combinatorics
that puts an upper bound on the chromatic number of a graph
(or hypergraph
in general). The original reference for this paper is unknown at the moment, and has been called folklore.
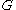acting on a set
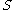is called transitive if given any two elements 
and 
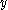in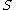 
, there exists an element 
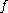of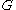 
such that 
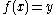. A graph (or hypergraph) is called symmetric if it's automorphism group is transitive.
Theorem. Let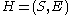
be a symmetric hypergraph. Let 
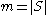, and let 
denote the chromatic number of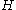 
, and let 
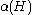denote the independence number of 
. Then
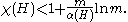
, specifically graph Ramsey theory. Using this theorem, a relationship between the graph Ramsey numbers and the extremal numbers can be shown (see Graham-Rothschild-Spencer for the details).
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
that puts an upper bound on the chromatic number of a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
(or hypergraph
Hypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
in general). The original reference for this paper is unknown at the moment, and has been called folklore.
Statement
A groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
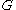acting on a setGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
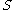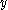is called transitive if given any two elements and in 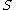, there exists an element 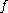of 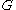such that 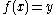. A graph (or hypergraph) is called symmetric if it's automorphism group is transitive.Theorem. Let
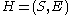be a symmetric hypergraph. Let 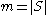, and let denote the chromatic number of 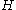, and let 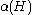denote the independence number of . Then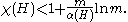Applications
This theorem has applications to Ramsey theoryRamsey theory
Ramsey theory, named after the British mathematician and philosopher Frank P. Ramsey, is a branch of mathematics that studies the conditions under which order must appear...
, specifically graph Ramsey theory. Using this theorem, a relationship between the graph Ramsey numbers and the extremal numbers can be shown (see Graham-Rothschild-Spencer for the details).