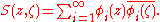Szegő kernel
Encyclopedia
In the mathematical
study of several complex variables
, the Szegő kernel is an integral kernel that gives rise to a reproducing kernel on a natural Hilbert space
of holomorphic function
s. It is named for its discoverer, the Hungarian mathematician Gábor Szegő
.
Let Ω be a bounded domain in Cn with C2 boundary, and let A(Ω) denote the set of all holomorphic functions in Ω that are continuous on . Define the Hardy space
. Define the Hardy space
H2(∂Ω) to be the closure in L2(∂Ω) of the restrictions of elements of A(Ω) to the boundary. The Poisson integral implies that each element ƒ of H2(∂Ω) extends to a holomorphic function Pƒ in Ω. Furthermore, for each z ∈ Ω, the map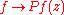
defines a continuous linear functional on H2(∂Ω). By the Riesz representation theorem
, this linear functional is represented by a kernel kz, which is to say
The Szegő kernel is defined by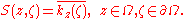
Like its close cousin, the Bergman kernel
, the Szegő kernel is holomorphic in z. In fact, if φi is an orthonormal basis
of H2(∂Ω) consisting entirely of the restrictions of functions in A(Ω), then a Riesz–Fischer theorem
argument shows that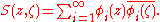
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
study of several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
, the Szegő kernel is an integral kernel that gives rise to a reproducing kernel on a natural Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s. It is named for its discoverer, the Hungarian mathematician Gábor Szegő
Gábor Szego
Gábor Szegő was a Hungarian mathematician. He was one of the foremost analysts of his generation and made fundamental contributions to the theory of Toeplitz matrices and orthogonal polynomials.-Life:...
.
Let Ω be a bounded domain in Cn with C2 boundary, and let A(Ω) denote the set of all holomorphic functions in Ω that are continuous on
 . Define the Hardy space
. Define the Hardy spaceHardy space
In complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
H2(∂Ω) to be the closure in L2(∂Ω) of the restrictions of elements of A(Ω) to the boundary. The Poisson integral implies that each element ƒ of H2(∂Ω) extends to a holomorphic function Pƒ in Ω. Furthermore, for each z ∈ Ω, the map
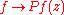
defines a continuous linear functional on H2(∂Ω). By the Riesz representation theorem
Riesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
, this linear functional is represented by a kernel kz, which is to say

The Szegő kernel is defined by
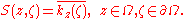
Like its close cousin, the Bergman kernel
Bergman kernel
In the mathematical study of several complex variables, the Bergman kernel, named after Stefan Bergman, is a reproducing kernel for the Hilbert space of all square integrable holomorphic functions on a domain D in Cn....
, the Szegő kernel is holomorphic in z. In fact, if φi is an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of H2(∂Ω) consisting entirely of the restrictions of functions in A(Ω), then a Riesz–Fischer theorem
Riesz–Fischer theorem
In mathematics, the Riesz–Fischer theorem in real analysis refers to a number of closely related results concerning the properties of the space L2 of square integrable functions...
argument shows that