In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, a tacnode is a kind of singular point of a curve

Singular point of a curve

In geometry, a singular point on a curve is one where the curve is not given by a smooth embedding of a parameter. The precise definition of a singular point depends on the type of curve being studied.-Algebraic curves in the plane:...

. It is defined as a point where two (or more) osculating circle

Osculating circle

In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p...

s to the curve at that point are tangent

Tangent

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...

. This means that two branches of the curve have ordinary tangency at the double point. The canonical example is A tacnode is then a point of self tangency locally

Local property

In mathematics, a phenomenon is sometimes said to occur locally if, roughly speaking, it occurs on sufficiently small or arbitrarily small neighborhoods of points.-Properties of a single space:...

 diffeomorphic to the origin in the case of

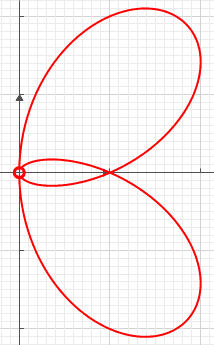
Another example of a tacnode is given by the links curve with equation 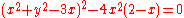. See the figure.

More general background

Consider a smooth

Smooth function

In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...

 real-valued function

Real-valued function

In mathematics, a real-valued function is a function that associates to every element of the domain a real number in the image....

 of two variable

Variable

Variable may refer to:* Variable , a logical set of attributes* Variable , a symbol that represents a quantity in an algebraic expression....

s, say f(x, y) where x and y are real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s. So f is a function from the plane to the line. The space of all such smooth functions is acted

Group action

In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...

 upon by the group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

 of diffeomorphism

Diffeomorphism

In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...

s of the plane and the diffeomorphisms of the line, i.e. diffeomorphic changes of coordinate in both the source and the target. This action splits the whole function space

Function space

In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...

 up into equivalence classes, i.e. orbits of the group action.

One such family of equivalence classes is denoted by A_k^±

Ak singularity

In mathematics, and in particular singularity theory an Ak, where k ≥ 0 is an integer, describes a level of degeneracy of a function. The notation was introduced by V. I. Arnold....

, where k is a non-negative integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

. This notation was introduced by V. I. Arnold. A function f is said to be of type A_k^±

Ak singularity

In mathematics, and in particular singularity theory an Ak, where k ≥ 0 is an integer, describes a level of degeneracy of a function. The notation was introduced by V. I. Arnold....

 if it lies in the orbit of x² ± y^k+1, i.e. there exists a diffeomorphic change of coordinate in source and target which takes f into one of these forms. These simple forms x² ± y^k+1 are said to give normal form

Canonical form

Generally, in mathematics, a canonical form of an object is a standard way of presenting that object....

s for the type A_k^±

Ak singularity

In mathematics, and in particular singularity theory an Ak, where k ≥ 0 is an integer, describes a level of degeneracy of a function. The notation was introduced by V. I. Arnold....

-singularities.

A curve with equation f = 0 will have a tacnode, say at the origin, if and only if f has a type A₃⁻-singularity at the origin.

Notice that a node (x² − y² = 0) corresponds to a type A₁⁻-singularity. A tacnode corresponds to a type A₃⁻-singularity. In fact each type A_2n+1⁻-singularity, where n ≥ 0 is an integer, corresponds to a curve with self intersection. As n increases the order of self intersection increases: transverse crossing, ordinary tangency, etc.

The type A_2n+1⁺-singularities are of no interest over the real numbers: they all give an isolated point. Over the complex numbers type A_2n+1⁺-singularities and type A_2n+1⁻-singularities are equivalent: (x,y) → (x, iy) gives the required diffeomorphism of the normal forms.