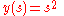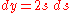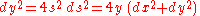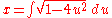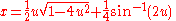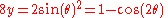Tautochrone curve
Encyclopedia

Cycloid
A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
, and the time is equal to π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
times the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
of the radius over the acceleration of gravity.
The tautochrone problem
The tautochrone problem, the attempt to identify this curve, was solved by Christiaan Huygens in 1659. He proved geometrically in his Horologium oscillatorium, originally published in 1673, that the curve was a cycloidCycloid
A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
.
- "On a cycloid whose axis is erected on the perpendicular and whose vertex is located at the bottom, the times of descent, in which a body arrives at the lowest point at the vertex after having departed from any point on the cycloid, are equal to each other..."
This solution was later used to attack the problem of the brachistochrone curve
Brachistochrone curve
A Brachistochrone curve , or curve of fastest descent, is the curve between two points that is covered in the least time by a point-like body that starts at the first point with zero speed and is constrained to move along the curve to the second point, under the action of constant gravity and...
. Jakob Bernoulli solved the problem using calculus in a paper (Acta Eruditorum
Acta Eruditorum
Acta Eruditorum was the first scientific journal of the German lands, published from 1682 to 1782....
, 1690) that saw the first published use of the term integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
.
The tautochrone problem was studied more closely when it was realized that a pendulum, which follows a circular path, was not isochronous
Isochronous
Isochronous : From Greek iso, equal + chronos, time. It literally means regularly, or at equal time intervals. In general English language, it refers to something that occurs at a regular interval, of the same duration; as opposed to synchronous which refers to more than one thing happening at the...
and thus his pendulum clock
Pendulum clock
A pendulum clock is a clock that uses a pendulum, a swinging weight, as its timekeeping element. The advantage of a pendulum for timekeeping is that it is a resonant device; it swings back and forth in a precise time interval dependent on its length, and resists swinging at other rates...
would keep different time depending on how far the pendulum swung. After determining the correct path, Christiaan Huygens attempted to create pendulum clocks that used a string to suspend the bob and curb cheeks near the top of the string to change the path to the tautochrone curve. These attempts proved to not be useful for a number of reasons. First, the bending of the string causes friction, changing the timing. Second, there were much more significant sources of timing errors that overwhelmed any theoretical improvements that traveling on the tautochrone curve helps. Finally, the "circular error" of a pendulum decreases as length of the swing decreases, so better clock escapement
Escapement
In mechanical watches and clocks, an escapement is a device that transfers energy to the timekeeping element and enables counting the number of oscillations of the timekeeping element...
s could greatly reduce this source of inaccuracy.
Later, the mathematicians Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
and Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
provided an analytical solution to the problem.
Lagrangian solution
If the particle's position is parametrized by the arclength s(t) from the lowest point, the kinetic energy is proportional to . The potential energy is proportional to the height y(s). In order to be an isochrone, the Lagrangian must be that of a simple harmonic oscillator: the height of the curve must be proportional to the arclength squared.
. The potential energy is proportional to the height y(s). In order to be an isochrone, the Lagrangian must be that of a simple harmonic oscillator: the height of the curve must be proportional to the arclength squared.where the constant of proportionality has been set to 1 by changing units of length.
The differential form of this relation is
Which eliminates s, and leaves a differential equation for dx and dy. To find the solution, integrate for x in terms of y:
Where
 . This integral is the area under a circle, which can be naturally cut into a triangle and a circular wedge:
. This integral is the area under a circle, which can be naturally cut into a triangle and a circular wedge:To see that this is a strangely parametrized cycloid
Cycloid
A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
, change variables to disentangle the transcendental and algebraic parts: define the angle
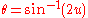 .
.Which is the standard parametrization, except for the scale of x, y and θ.
"Virtual gravity" solution
Perhaps the simplest solution to the tautochrone problem is to note a direct relation between the angle of an incline and the gravity felt by a particle on the incline. A particle on a 90° vertical incline feels the full effect of gravity, while a particle on a horizontal plane feels effectively no gravity. At intermediate angles, the "virtual gravity" felt by the particle is g sin θ. The first step is to find a "virtual gravity" that produces the desired behavior.The "virtual gravity" required for the tautochrone is simply proportional to the distance remaining to be traveled, which admits a simple solution:

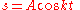
It can be easily verified both that this solution solves the differential equation and that a particle will reach s = 0 at time π/(2k) from any starting height A. The problem is now to construct a curve that will produce a "virtual gravity" proportional to the distance remaining to travel, i.e., a curve that satisfies:

The explicit appearance of the distance remaining is troublesome, but we can differentiate
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
to obtain a more manageable form:

or

This equation relates the change in the curve's angle to the change in the distance along the curve. We now use the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
, the fact that the slope of the curve is equal to the tangent of its angle, and some trigonometric identities to obtain ds in terms of dx:
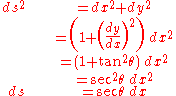
Substituting this into the first differential equation lets us solve for x in terms of θ:
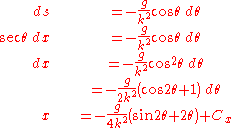
Likewise, we can also express dx in terms of dy and solve for y in terms of θ:
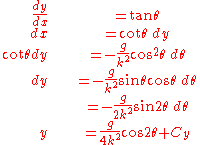
Substituting
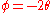 and
and 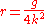 , we see that these equations for
, we see that these equations for  and
and  are those of a circle rolling along a horizontal line — a cycloid
are those of a circle rolling along a horizontal line — a cycloidCycloid
A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
:
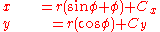
Solving for k and remembering that
 is the time required for descent, we find the descent time in terms of the radius r:
is the time required for descent, we find the descent time in terms of the radius r: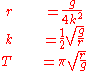
(Based loosely on Proctor, pp. 135–139)
Abel's solution
Niels Henrik AbelNiels Henrik Abel
Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
attacked a generalized version of the tautochrone problem (Abel's mechanical problem), namely, given a function T(y) that specifies the total time of descent for a given starting height, find an equation of the curve that yields this result. The tautochrone problem is a special case of Abel's mechanical problem when T(y) is a constant.
Abel's solution begins with the principle of conservation of energy
Conservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
— since the particle is frictionless, and thus loses no energy to heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
, its kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
at any point is exactly equal to the difference in potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
from its starting point. The kinetic energy is
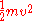 , and since the particle is constrained to move along a curve, its velocity is simply
, and since the particle is constrained to move along a curve, its velocity is simply 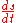 , where
, where  is the distance measured along the curve. Likewise, the gravitational potential energy gained in falling from an initial height
is the distance measured along the curve. Likewise, the gravitational potential energy gained in falling from an initial height 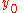 to a height
to a height 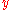 is
is 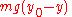 , thus:
, thus: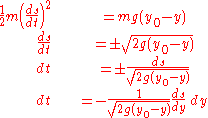
In the last equation, we've anticipated writing the distance remaining along the curve as a function of height (s(y)), recognized that the distance remaining must decrease as time increases (thus the minus sign), and used the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
in the form
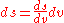 .
.Now we integrate from
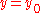 to
to  to get the total time required for the particle to fall:
to get the total time required for the particle to fall: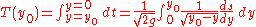
This is called Abel's integral equation and allows us to compute the total time required for a particle to fall along a given curve (for which
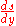 would be easy to calculate). But Abel's mechanical problem requires the converse — given
would be easy to calculate). But Abel's mechanical problem requires the converse — given 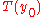 , we wish to find
, we wish to find 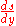 , from which an equation for the curve would follow in a straightforward manner. To proceed, we note that the integral on the right is the convolution
, from which an equation for the curve would follow in a straightforward manner. To proceed, we note that the integral on the right is the convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of
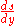 with
with 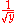 and thus take the Laplace transform of both sides:
and thus take the Laplace transform of both sides: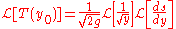
Since
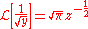 , we now have an expression for the Laplace transform of
, we now have an expression for the Laplace transform of 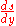 in terms of
in terms of 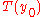 's Laplace transform:
's Laplace transform: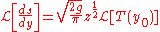
This is as far as we can go without specifying
 . Once
. Once  is known, we can compute its Laplace transform, calculate the Laplace transform of
is known, we can compute its Laplace transform, calculate the Laplace transform of 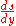 and then take the inverse transform (or try to) to find
and then take the inverse transform (or try to) to find 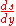 .
.For the tautochrone problem,
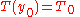 is constant. Since the Laplace transform of 1 is
is constant. Since the Laplace transform of 1 is 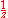 , we continue:
, we continue: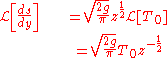
Making use again of the Laplace transform above, we invert the transform and conclude:
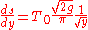
It can be shown that the cycloid obeys this equation.
(Simmons, Section 54).
See also
- Calculus of variationsCalculus of variationsCalculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
- Beltrami identityBeltrami identityThe Beltrami identity is an identity in the calculus of variations. It says that a function u which is an extremal of the integralI=\int_a^b L \, dxsatisfies the differential equation...
- CycloidCycloidA cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
- Tautochrone curveTautochrone curveA tautochrone or isochrone curve is the curve for which the time taken by an object sliding without friction in uniform gravity to its lowest point is independent of its starting point...
- CatenaryCatenaryIn physics and geometry, the catenary is the curve that an idealised hanging chain or cable assumes when supported at its ends and acted on only by its own weight. The curve is the graph of the hyperbolic cosine function, and has a U-like shape, superficially similar in appearance to a parabola...
- uniformly accelerated motion