Tensor-hom adjunction
Encyclopedia
In mathematics
, the tensor-hom adjunction is that the functor
s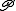
and 
form an adjoint pair: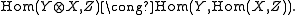
This is made more precise below. The order "tensor-hom adjunction" is because tensor is the left adjoint, while hom is the right adjoint.
, and consider the right module
categories C = Mod-R and D = Mod-S. Fix a bimodule A=RAS. The functor
taking XR to the tensor product
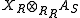is left adjoint
to the functor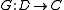
taking YS to Hom
S(RAS, YS).
An analogous statement holds for left modules.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the tensor-hom adjunction is that the functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s
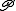and form an adjoint pair: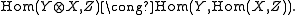This is made more precise below. The order "tensor-hom adjunction" is because tensor is the left adjoint, while hom is the right adjoint.
General Statement
Say R and S are (possibly noncommutative) ringsRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, and consider the right module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
categories C = Mod-R and D = Mod-S. Fix a bimodule A=RAS. The functor
taking XR to the tensor productTensor product of modules
In mathematics, the tensor product of modules is a construction that allows arguments about bilinear maps to be carried out in terms of linear maps...
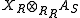is left adjointAdjoint functors
In mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
to the functor
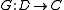taking YS to HomHom functor
In mathematics, specifically in category theory, hom-sets, i.e. sets of morphisms between objects, give rise to important functors to the category of sets. These functors are called hom-functors and have numerous applications in category theory and other branches of mathematics.-Formal...
S(RAS, YS).
An analogous statement holds for left modules.