Tetrated dodecahedron
Type	near-miss Johnson solid Near-miss Johnson solid In geometry, a near-miss Johnson solid is a strictly convex polyhedron, where every face is a regular or nearly regular polygon, and excluding the 5 Platonic solids, the 13 Archimedean solids, the infinite set of prisms, the infinite set of antiprisms, and the 92 Johnson solids.The set of...
Faces	4+12 triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... s 12 pentagon Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... s
Edges	54
Vertices	28
Vertex configuration Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron...	4 (5.5.5) 12 (3.5.3.5) 12 (3.3.5.5)
Symmetry group	Td
Properties	convex

The tetrated dodecahedron is a near-miss Johnson solid

Near-miss Johnson solid

In geometry, a near-miss Johnson solid is a strictly convex polyhedron, where every face is a regular or nearly regular polygon, and excluding the 5 Platonic solids, the 13 Archimedean solids, the infinite set of prisms, the infinite set of antiprisms, and the 92 Johnson solids.The set of...

. It was first discovered in 2002 by Alex Doskey. It was then independently rediscovered in 2003 and named by Robert Austin.

It has 28 faces: twelve regular pentagons arranged in four panels of three pentagons each, four equilateral triangles (shown in blue), and six pairs of isosceles triangles (shown in yellow). All edges of the tetrated dodecahedron have the same length, except for the shared bases of these isosceles triangles, which are approximately 1.07 times as long as the other edges. This polyhedron

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

 has tetrahedral symmetry

Tetrahedral symmetry

150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...

.

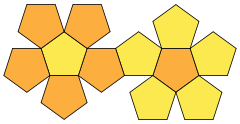
Net

The 12 pentagons and 16 triangles are colored in this net by their locations within the tetrahedral symmetry.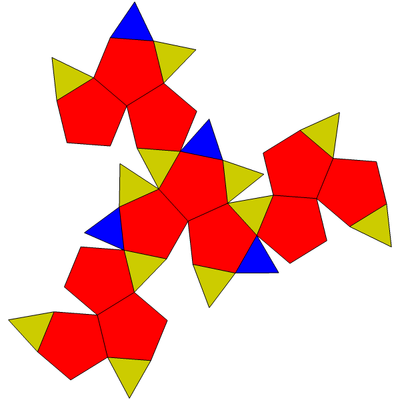

Related polyhedra

Dodecahedron (Platonic solid Platonic solid In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and... )	Icosidodecahedron Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon... (Archimedean solid Archimedean solid In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices... )	Pentagonal orthobirotunda Pentagonal orthobirotunda In geometry, the pentagonal orthobirotunda is one of the Johnson solids . As the name suggests, it can be constructed by joining two pentagonal rotundae along their decagonal faces, matching like faces... (Johnson solid Johnson solid In geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around... )