All Topics  
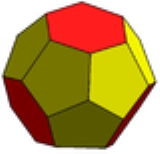
Near-miss Johnson solid

 

 
   Email Print
   Bookmark   Link
 

 

Near-miss Johnson solid
 
 
  Topics Near-miss Johnson solid Topic Home

In geometry
Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers....
, a near-miss Johnson solid is a strictly convex
Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object....
 polyhedron
Polyhedron

|}A polyhedron is often defined as a geometry object with flat faces and straight edges .This definition of a polyhedron is not very precise, and to a modern mathematician is quite unsatisfactory....
, where every face is a regular or nearly regular polygon
Regular polygon

A regular polygon is a polygon which is Equiangular polygon and equilateral . Regular polygons may be convex or Star polygon....
, and excluding the 5 Platonic solid
Platonic solid

In geometry, a Platonic solid is a convex set polyhedron that is regular polyhedron, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruence regular polygons, with the same number of faces meeting at each vertex....
s, the 13 Archimedean solid
Archimedean solid

In geometry an Archimedean solid is a highly symmetric, semi-regular convex set polyhedron composed of two or more types of regular polygons meeting in identical vertex ....
s, the infinite set of prism
Prism (geometry)

In geometry, an n-sided prism is a polyhedron made of an n-sided polygon base, a Translation copy, and n faces joining corresponding sides....
s, the infinite set of antiprism
Antiprism

An n-sided antiprism is a polyhedron composed of 2 parallel copies of some particular n-sided polygon, connected by an alternating band of triangles....
s, and the 92 Johnson solid
Johnson solid

In geometry, a Johnson solid is a strictly convex set polyhedron, each face of which is a regular polygon, but which is not uniform polyhedron, i.e., not a Platonic solid, Archimedean solid, prism or antiprism....
s.

The set of near-misses is not exactly defined, but can be loosely defined as convex polyhedra that can be approximately constructed from rigid regular polygon faces as a physical model. Because of the "fuzziness" of this definition, the exact number of near-misses is not known.

Examples
These four convex polyhedra can be modelled physically with regular polygon faces with various degrees of adjustment.






Discussion
Ask a question about 'Near-miss Johnson solid'
Start a new discussion about 'Near-miss Johnson solid'
Answer questions from other users
Full Discussion Forum



Encyclopedia


In geometry
Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers....
, a near-miss Johnson solid is a strictly convex
Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object....
 polyhedron
Polyhedron

|}A polyhedron is often defined as a geometry object with flat faces and straight edges .This definition of a polyhedron is not very precise, and to a modern mathematician is quite unsatisfactory....
, where every face is a regular or nearly regular polygon
Regular polygon

A regular polygon is a polygon which is Equiangular polygon and equilateral . Regular polygons may be convex or Star polygon....
, and excluding the 5 Platonic solid
Platonic solid

In geometry, a Platonic solid is a convex set polyhedron that is regular polyhedron, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruence regular polygons, with the same number of faces meeting at each vertex....
s, the 13 Archimedean solid
Archimedean solid

In geometry an Archimedean solid is a highly symmetric, semi-regular convex set polyhedron composed of two or more types of regular polygons meeting in identical vertex ....
s, the infinite set of prism
Prism (geometry)

In geometry, an n-sided prism is a polyhedron made of an n-sided polygon base, a Translation copy, and n faces joining corresponding sides....
s, the infinite set of antiprism
Antiprism

An n-sided antiprism is a polyhedron composed of 2 parallel copies of some particular n-sided polygon, connected by an alternating band of triangles....
s, and the 92 Johnson solid
Johnson solid

In geometry, a Johnson solid is a strictly convex set polyhedron, each face of which is a regular polygon, but which is not uniform polyhedron, i.e., not a Platonic solid, Archimedean solid, prism or antiprism....
s.

The set of near-misses is not exactly defined, but can be loosely defined as convex polyhedra that can be approximately constructed from rigid regular polygon faces as a physical model. Because of the "fuzziness" of this definition, the exact number of near-misses is not known.

Examples


These four convex polyhedra can be modelled physically with regular polygon faces with various degrees of adjustment. If they could be built exactly, they would be Johnson solids.

Name Imageverfs
Vertex figure

In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off....
 V E F F3 F4 F5 F6 F8 F10 Symmetry
List of spherical symmetry groups

List of symmetry groups on the sphere Spherical symmetry groups are also called point groups in three dimensions. This article is about Point_groups_in_three_dimensions#Finite_isometry_groups....
Truncated triakis tetrahedron
Truncated triakis tetrahedron

The truncated triakis tetrahedron is a convex polyhedron with 16 faces: 4 sets of 3 pentagons arranged in a Tetrahedral symmetry arrangement, with 4 hexagons in the gaps....
4 (5.5.5)
24 (5.5.6)		 28 42 16     12 4     Td
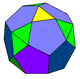-- 6 (5.5.5)
9 (3.5.3.5)
12 (3.3.5.5)		 27 51 26 14   12       D3h
Tetrated dodecahedron
Tetrated dodecahedron

The tetrated dodecahedron is a near-miss Johnson solid. It was first discovered in 2002 by Alex Doskey. It was then independently rediscovered in 2003 and named by Robert Austin....
4 (5.5.5)
12 (3.5.3.5)
12 (3.3.5.5)		 28 54 28 16   12       Td
--
Hexpenttri Near Miss Johnson Solid
12 (5.5.6)
6 (3.5.3.5)
12 (3.3.5.5)		 30 54 26 12   12 2     D6h


Possible vertex figures


The near-misses, like all convex polyhedra made of regular polygons, have a countably infinite set of vertex figure
Vertex figure

In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off....
s that they can use, defined by a positive angle defect
Defect (geometry)

In geometry, the defect of a vertex of a polyhedron is the amount by which the sum of the angles of the faces at the vertex falls short of a full circle....
. A secondary constraint for the triples requires the angle sum of the two smaller polygons to exceed the angle of the larger one.

The set of polygons that can create convex vertex figures include:
  • Triples p.q.r:
    • 3.3.(3-5), 3.4.(4-11), 3.5.(5-7), 3.6.(6+), 3.7.(7-41), 3.8.(8-23), 3.9.(9-17), 3.10.(10-14), 3.11.(11-13), 4.4.(4+), 4.5.(5-19), 4.6.(6-11), 4.7.(7-9), 5.5.(5-9), 5.6.(6-7).
  • Quadruples p.q.r.s:
    • 3.3.3.(3+), 3.3.4.(4-11), 3.3.5.(5-7), 3.4.4.(4-5)
  • Quintuples p.q.r.s.t:
    • 3.3.3.3.(3-5)


NOTE:
  • (a-b) means any polygon for which the number of sides is between a and b inclusive.
  • (n+) means any polygon with n or more sides.


Permutation
Permutation

In several fields of mathematics the term permutation is used with different but closely related meanings. They all relate to the notion of mapping the element s of a set to other elements of the same set, i.e., exchanging elements of a set....
s of these polygon lists further extend possible vertex figures.

Each vertex figure has an angle defect, and a convex polyhedron will have a combined angle defect of 720 degrees.

These vertex figures and angle defect sums contrain the possible existence of convex polyhedra of regular or near regular polygon faces.

See Vertex configuration
Vertex configuration

In polyhedral geometry a vertex configuration is a short-hand notation for representing a polyhedron vertex figure as the sequence of faces around a vertex....
 for the convex vertex figures used in the regular and semiregular solids.

See also

  • Platonic solid
    Platonic solid

    In geometry, a Platonic solid is a convex set polyhedron that is regular polyhedron, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruence regular polygons, with the same number of faces meeting at each vertex....
  • Semiregular polyhedron
    Semiregular polyhedron

    A semiregular polyhedron is a polyhedron with regular polygon faces and a symmetry group which is transitive on its vertices. Or at least, that is what follows from Thorold Gosset's 1900 definition of the more general semiregular polytope....
    • Archimedean solid
      Archimedean solid

      In geometry an Archimedean solid is a highly symmetric, semi-regular convex set polyhedron composed of two or more types of regular polygons meeting in identical vertex ....
    • prism
      Prism (geometry)

      In geometry, an n-sided prism is a polyhedron made of an n-sided polygon base, a Translation copy, and n faces joining corresponding sides....
    • antiprism
      Antiprism

      An n-sided antiprism is a polyhedron composed of 2 parallel copies of some particular n-sided polygon, connected by an alternating band of triangles....
  • Johnson solids
  • Geodesic dome
    Geodesic dome

    A geodesic dome is a spherical or partial-spherical thin-shell structure based on a network of great circles lying on the surface of a sphere....


External links