In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

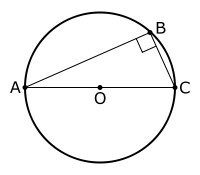
, Thales' theorem (named after Thales of Miletus) states that if A, B and C are points on a circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

 where the line AC is a diameter

Diameter

In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...

 of the circle, then the angle

Angle

In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...

 ABC is a right angle

Right angle

In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...

. Thales' theorem is a special case of the inscribed angle theorem. It is generally attributed to Thales, who is said to have sacrificed an ox in honor of the discovery, but sometimes it is attributed to Pythagoras

Pythagoras

Pythagoras of Samos was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him...

.

Proof

We use the following facts:

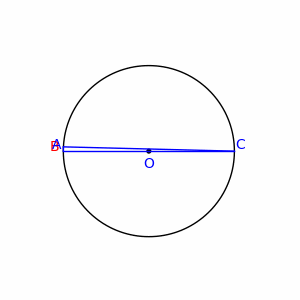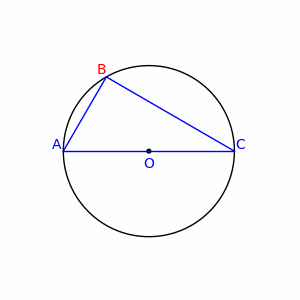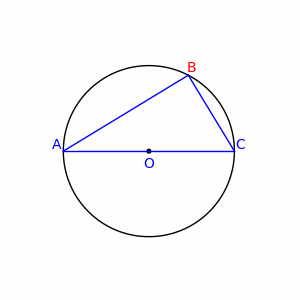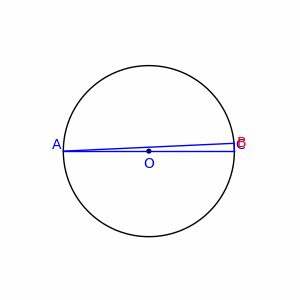
• the sum of the angles in a triangle
  Triangle
  A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
  
   is equal to two right angles (180°
  Degree (angle)
  A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...
  
  ),
• the base angles of an isosceles triangle are equal.

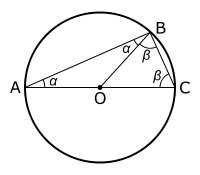
Let O be the center of the circle. Since OA = OB = OC, OBA and OBC are isosceles triangles, and by the equality of the base angles of an isosceles triangle, OBC = OCB and BAO = ABO. Let α = BAO and β = OBC. The three internal angles of the ABC triangle are α, α + β and β. Since the sum of the angles of a triangle is equal to two right angles, we have


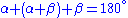
then


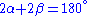
or simply


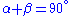
Q.E.D.

Q.E.D.

Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...

Converse

The converse of Thales' theorem is also valid; it states that a right triangle

Right triangle

A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...

's hypotenuse

Hypotenuse

In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...

 is a diameter of its circumcircle.

Combining Thales' theorem with its converse we get that:

The center of a triangle's circumcircle lies on one of the triangle's sides if and only if

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

 the triangle is a right triangle.

Proof of the converse using geometry

This proof consists of 'completing' the right triangle to form a rectangle

Rectangle

In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...

 and noticing that the center of that rectangle is equidistant from the vertices and so is the center of the circumscribing circle of the original triangle, it utilizes two facts:

• adjacent angles in a parallelogram
  Parallelogram
  In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
  
   are supplementary (add to 180°
  Degree (angle)
  A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...
  
  ) and,
• the diagonals of a rectangle are equal and cross each other in their median point.

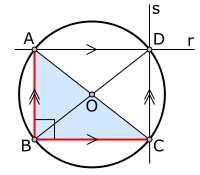
Let there be a right angle ABC, r a line parallel to BC passing by A and s a line parallel to AB passing by C. Let D be the point of intersection of lines r and s (Note that it has not been proven that D lies on the circle)

The quadrilateral ABCD forms a parallelogram by construction (as opposite sides are parallel). Since in a parallelogram adjacent angles are supplementary (add to 180°) and ABC is a right angle (90°) then angles BAD, BCD, and ADC are also right (90°); consequently ABCD is a rectangle.

Let O be the point of intersection of the diagonals AC and BD. Then the point O, by the second fact above, is equidistant from A,B, and C. And so O is center of the circumscribing circle, and the hypotenuse of the triangle AC is a diameter of the circle.

Proof of the converse using linear algebra

This proof utilizes two facts:

• two lines form a right angle if and only if the dot product
  Dot product
  In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
  
   of their directional vectors is zero, and
• the square of the length of a vector is given by the dot product of the vector with itself.

Let there be a right angle ABC and circle M with AC as a diameter.
Let M's center lie on the origin, for easier calculation.
Then we know

• A = − C, because the circle centered at the origin has AC as diameter, and
• (A − B) · (B − C) = 0, because ABC is a right angle.

It follows

0 = (A − B) · (B − C) = (A − B) · (B + A) = |A|² − |B|².

Hence:

|A| = |B|.

This means that A and B are equidistant from the origin, i.e. from the center of M. Since A lies on M, so does B, and the circle M is therefore the triangle's circumcircle.

The above calculations in fact establish that both directions of Thales' theorem are valid in any inner product space

Inner product space

In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...

.

Generalization

Thales' theorem is a special case of the following theorem:

Given three points A, B and C on a circle with center O, the angle AOC is twice as large as the angle ABC.

See inscribed angle

Inscribed angle

In geometry, an inscribed angle is formed when two secant lines of a circle intersect on the circle....

, the proof of this theorem is quite similar to the proof of Thales' theorem given above.

Application

Thales' theorem can be used to construct the tangent

Tangent

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...

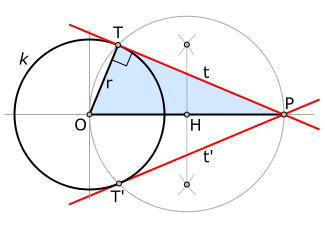
 to a given circle that passes through a given point. (See figure.)
Given a circle k, with a center O, and a point P outside of the circle, we want to construct the (red) tangent(s) to k that pass through P. Suppose the (as yet unknown) tangent t touches the circle in the point T. From symmetry, it is clear that the radius OT is orthogonal to the tangent. So construct the midpoint H between O and P, and draw a circle centered at H through O and P. By Thales' theorem, the sought point T is the intersection of this circle with the given circle k, because that is the point on k that completes a right triangle OTP.

Since there the two circles intersect at two points, we can construct both tangents in this fashion.

History

Thales was not the first to discover this theorem since the Egyptian

Egyptian mathematics

Egyptian mathematics is the mathematics that was developed and used in Ancient Egypt from ca. 3000 BC to ca. 300 BC.-Overview:Written evidence of the use of mathematics dates back to at least 3000 BC with the ivory labels found at Tomb Uj at Abydos. These labels appear to have been used as tags for...

s and Babylonian

Babylonian mathematics

Babylonian mathematics refers to any mathematics of the people of Mesopotamia, from the days of the early Sumerians to the fall of Babylon in 539 BC. Babylonian mathematical texts are plentiful and well edited...

s must have known of this empirically, however there is no record of a proof of the theorem by either of them. The theorem is named after Thales because he was said to have been the first to prove the theorem, using his own results that the base angles of an isosceles triangle are equal, and that the sum of angles in a triangle is equal to two right angles.

External links

• Munching on Inscribed Angles
• Thales' theorem explained With interactive animation
• Thales' Theorem by Michael Schreiber, The Wolfram Demonstrations Project.