Inscribed angle
Encyclopedia
In geometry
, an inscribed angle is formed when two secant line
s of a circle
(or, in a degenerate case, when one secant line
and one tangent line of that circle) intersect on the circle.
Typically, it is easiest to think of an inscribed angle as being defined by two chords
of the circle sharing an endpoint
.
The basic properties of inscribed angles are discussed in Book 4, Propositions 20-22 of Euclid's Elements
. These are the inscribed angle is half the central angle, inscribed angles on the same arc of a chord are equal and the sum of the two distinct inscribed angles of a chord is 180°.
on the circle. The arc is the portion of the circle that is in the interior of the angle. The measure of the intercepted arc (equal to its central angle
) is exactly twice the measure of the inscribed angle.
This single property has a number of consequences within the circle. For example, it allows one to prove that when two chords intersect in a circle, the products of the lengths of their pieces are equal. It also allows one to prove that the opposite angles of a cyclic quadrilateral
are supplementary
.
Let O be the center of a circle. Choose two points on the circle, and call them V and A. Draw line VO and extended past O so that it intersects the circle at point B which is diametrically opposite the point V. Draw an angle whose vertex is point V and whose sides pass through points A and B.
Angle BOA is a central angle
; call it θ. Draw line OA. Lines OV and OA are both radii
of the circle, so they have equal lengths. Therefore triangle VOA is isosceles, so angle BVA (the inscribed angle) and angle VAO are equal; let each of them be denoted as ψ.
Angles BOA and AOV are supplementary. They add up to 180°, since line VB passing through O is a straight line. Therefore angle AOV measures 180° − θ.
It is known that the three angles of a triangle
add up to 180°, and the three angles of triangle VOA are:
Therefore
Subtract 180° from both sides,
where θ is the central angle subtending arc AB and ψ is the inscribed angle subtending arc AB.
Suppose this arc includes point E within it. Point E is diametrically opposite to point V. Angles DVE and EVC are also inscribed angles, but both of these angles have one side which passes through the center of the circle, therefore the theorem from the above Part 1 can be applied to them.
Therefore
then let
so that
Draw lines OC and OD. Angle DOC is a central angle, but so are angles DOE and EOC, and
Let
so that
From Part One we know that
and that 
. Combining these results with equation (2) yields
therefore, by equation (1),
Given a circle whose center is point O, choose three points V, C, and D on the circle. Draw lines VC and VD: angle DVC is an inscribed angle. Now draw line VO and extend it past point O so that it intersects the circle at point E. Angle DVC subtends arc DC on the circle.
Suppose this arc does not include point E within it. Point E is diametrically opposite to point V. Angles DVE and EVC are also inscribed angles, but both of these angles have one side which passes through the center of the circle, therefore the theorem from the above Part 1 can be applied to them.
Therefore
.
then let
so that
Draw lines OC and OD. Angle DOC is a central angle, but so are angles DOE and EOC, and
Let
so that
From Part One we know that
and that 
. Combining these results with equation (4) yields
therefore, by equation (3),
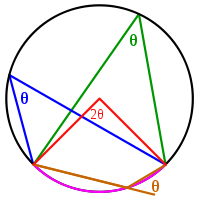The inscribed angle theorem states that an angle θ inscribed in a circle is half of the central angle 2θ that subtends the same arc
on the circle. Therefore, the angle does not change as its apex
is moved to different positions on the circle.
The inscribed angle theorem
is used in many proofs of elementary Euclidean geometry of the plane. A special case of the theorem is Thales' theorem
, which states that the angle subtended by a diameter
is always 90°, i.e., a right angle. As a consequence of the theorem, opposite angles of cyclic quadrilateral
s sum to 180°; conversely, any quadrilateral for which this is true can be inscribed in a circle. As another example, the inscribed angle theorem is the basis for several theorems related to the power of a point
with respect to a circle.
from the center of the circle to the other point of intersection
of the inscribed angle produces an isoceles triangle, made from two radii of the circle and the second leg of the inscribed angle. Since two angles in an isoceles triangle are equal and since the angles in a triangle must add up to 180°, it follows that the inscribed angle equals θ, half of the central angle.
This result may be extended to arbitrary inscribed angles by drawing a diameter from its apex. This converts the general problem into two sub-cases in which a diameter is a leg. Adding the two subangles again yields the result that the inscribed angle is half of the central angle.
Note, that the central angle for the golden inscribed angle is 360°-2θ. Therefore, the half of it (and thus the measure of the golden inscribed angle) is 180°-θ.
The set of all points (locus) for which a line segment can be seen at angle measured θ contains two arcs (one of each side of the line segment with central angle 2θ). In the special case of 90°, we get exactly one circle with center the middle of the line segment
and the tangent
line at one of its intersection points equals half of the central angle subtended by the chord. See also Tangent lines to circles
.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, an inscribed angle is formed when two secant line
Secant line
A secant line of a curve is a line that intersects two points on the curve. The word secant comes from the Latin secare, to cut.It can be used to approximate the tangent to a curve, at some point P...
s of a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
(or, in a degenerate case, when one secant line
Secant line
A secant line of a curve is a line that intersects two points on the curve. The word secant comes from the Latin secare, to cut.It can be used to approximate the tangent to a curve, at some point P...
and one tangent line of that circle) intersect on the circle.
Typically, it is easiest to think of an inscribed angle as being defined by two chords
Chord (geometry)
A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
of the circle sharing an endpoint
Endpoint
An endpoint or end point is a mark of termination or completion.* In geometry, an endpoint is a point at which a line segment or ray terminates* Endpoint , the conclusion of a chemical reaction, particularly for titration...
.
The basic properties of inscribed angles are discussed in Book 4, Propositions 20-22 of Euclid's Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
. These are the inscribed angle is half the central angle, inscribed angles on the same arc of a chord are equal and the sum of the two distinct inscribed angles of a chord is 180°.
Property
An inscribed angle is said to intersect an arcArc (geometry)
In geometry, an arc is a closed segment of a differentiable curve in the two-dimensional plane; for example, a circular arc is a segment of the circumference of a circle...
on the circle. The arc is the portion of the circle that is in the interior of the angle. The measure of the intercepted arc (equal to its central angle
Central angle
A central angle is an angle which vertex is the center of a circle, and whose sides pass through a pair of points on the circle, thereby subtending an arc between those two points whose angle is equal to the central angle itself...
) is exactly twice the measure of the inscribed angle.
This single property has a number of consequences within the circle. For example, it allows one to prove that when two chords intersect in a circle, the products of the lengths of their pieces are equal. It also allows one to prove that the opposite angles of a cyclic quadrilateral
Cyclic quadrilateral
In Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
are supplementary
Supplementary angles
Supplementary angles are pairs of angles that add up to 180 degrees. Thus the supplement of an angle of x degrees is an angle of degrees....
.
Inscribed angles where one chord is a diameter
Let O be the center of a circle. Choose two points on the circle, and call them V and A. Draw line VO and extended past O so that it intersects the circle at point B which is diametrically opposite the point V. Draw an angle whose vertex is point V and whose sides pass through points A and B.
Angle BOA is a central angle
Central angle
A central angle is an angle which vertex is the center of a circle, and whose sides pass through a pair of points on the circle, thereby subtending an arc between those two points whose angle is equal to the central angle itself...
; call it θ. Draw line OA. Lines OV and OA are both radii
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
of the circle, so they have equal lengths. Therefore triangle VOA is isosceles, so angle BVA (the inscribed angle) and angle VAO are equal; let each of them be denoted as ψ.
Angles BOA and AOV are supplementary. They add up to 180°, since line VB passing through O is a straight line. Therefore angle AOV measures 180° − θ.
It is known that the three angles of a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
add up to 180°, and the three angles of triangle VOA are:
- 180° − θ
- ψ
- ψ.
Therefore
Subtract 180° from both sides,
where θ is the central angle subtending arc AB and ψ is the inscribed angle subtending arc AB.
Inscribed angles with the center of the circle in their interior
Given a circle whose center is point O, choose three points V, C, and D on the circle. Draw lines VC and VD: angle DVC is an inscribed angle. Now draw line VO and extend it past point O so that it intersects the circle at point E. Angle DVC subtends arc DC on the circle.Suppose this arc includes point E within it. Point E is diametrically opposite to point V. Angles DVE and EVC are also inscribed angles, but both of these angles have one side which passes through the center of the circle, therefore the theorem from the above Part 1 can be applied to them.
Therefore
then let
so that
Draw lines OC and OD. Angle DOC is a central angle, but so are angles DOE and EOC, and
Let
so that
From Part One we know that
and that . Combining these results with equation (2) yieldstherefore, by equation (1),
Inscribed angles with the center of the circle in their exterior
[The previous case can be extended to cover the case where the measure of the inscribed angle is the difference between two inscribed angles as discussed in the first part of this proof.]Given a circle whose center is point O, choose three points V, C, and D on the circle. Draw lines VC and VD: angle DVC is an inscribed angle. Now draw line VO and extend it past point O so that it intersects the circle at point E. Angle DVC subtends arc DC on the circle.
Suppose this arc does not include point E within it. Point E is diametrically opposite to point V. Angles DVE and EVC are also inscribed angles, but both of these angles have one side which passes through the center of the circle, therefore the theorem from the above Part 1 can be applied to them.
Therefore
.then let
so that
Draw lines OC and OD. Angle DOC is a central angle, but so are angles DOE and EOC, and
Let
so that
From Part One we know that
and that . Combining these results with equation (4) yieldstherefore, by equation (3),
Theorem
Arc (geometry)
In geometry, an arc is a closed segment of a differentiable curve in the two-dimensional plane; for example, a circular arc is a segment of the circumference of a circle...
on the circle. Therefore, the angle does not change as its apex
Apex (geometry)
In geometry, an apex is the vertex which is in some sense the highest of the figure to which it belongs.*In an isosceles triangle, the apex is the vertex where the two sides of equal length meet, opposite the unequal third side....
is moved to different positions on the circle.
The inscribed angle theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
is used in many proofs of elementary Euclidean geometry of the plane. A special case of the theorem is Thales' theorem
Thales' theorem
In geometry, Thales' theorem states that if A, B and C are points on a circle where the line AC is a diameter of the circle, then the angle ABC is a right angle. Thales' theorem is a special case of the inscribed angle theorem...
, which states that the angle subtended by a diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
is always 90°, i.e., a right angle. As a consequence of the theorem, opposite angles of cyclic quadrilateral
Cyclic quadrilateral
In Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
s sum to 180°; conversely, any quadrilateral for which this is true can be inscribed in a circle. As another example, the inscribed angle theorem is the basis for several theorems related to the power of a point
Power of a point
In elementary plane geometry, the power of a point is a real number h that reflects the relative distance of a given point from a given circle. Specifically, the power of a point P with respect to a circle C of radius r is defined...
with respect to a circle.
Proof
In the simplest case, one leg of the inscribed angle is a diameter of the circle, i.e., passes through the center of the circle. Since that leg is a straight line, the supplement of the central angle equals 180°−2θ. Drawing a segmentCircular segment
In geometry, a circular segment is an area of a circle informally defined as an area which is "cut off" from the rest of the circle by a secant or a chord. The circle segment constitutes the part between the secant and an arc, excluding the circle's center...
from the center of the circle to the other point of intersection
Line-line intersection
In Euclidean geometry, the intersection of a line and a line can be the empty set,a point, ora line. Distinguishing these cases, and finding the intersection point have use, for example, in computer graphics, motion planning, and collision detection....
of the inscribed angle produces an isoceles triangle, made from two radii of the circle and the second leg of the inscribed angle. Since two angles in an isoceles triangle are equal and since the angles in a triangle must add up to 180°, it follows that the inscribed angle equals θ, half of the central angle.
This result may be extended to arbitrary inscribed angles by drawing a diameter from its apex. This converts the general problem into two sub-cases in which a diameter is a leg. Adding the two subangles again yields the result that the inscribed angle is half of the central angle.
Note, that the central angle for the golden inscribed angle is 360°-2θ. Therefore, the half of it (and thus the measure of the golden inscribed angle) is 180°-θ.
The set of all points (locus) for which a line segment can be seen at angle measured θ contains two arcs (one of each side of the line segment with central angle 2θ). In the special case of 90°, we get exactly one circle with center the middle of the line segment
Corollaries
By a similar argument, the angle between a chordChord (geometry)
A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
and the tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
line at one of its intersection points equals half of the central angle subtended by the chord. See also Tangent lines to circles
Tangent lines to circles
In Euclidean plane geometry, tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs...
.
External links
- Relationship Between Central Angle and Inscribed Angle
- Munching on Inscribed Angles at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Arc Central Angle With interactive animation
- Arc Peripheral (inscribed) Angle With interactive animation
- Arc Central Angle Theorem With interactive animation